ブラックショールズモデルから色々考えてみた

この3年ある独自理論でオプション取引をやり続けた結果儲からなかった(笑)
これは理論自体が破綻しているという意味ではなく、当該理論では儲けられる時もあれば儲けられない時もあるという至極当たり前の意味でである
破綻している理論なら損を出し続けるだろう。また、結局裁量が介在してしまうためにせっかくの理論も意味がなかったりする、ということが改めて分かる
更に言えばオプション価格と言うものはその価格で買い続けても売り続けても長い期間のトータルでは損益ゼロに収束していくということに気付く
逆に言えばやはり相場勘というかその時々の相場環境に合わせて適時適切なトレードをしなければ儲からないわけである
当たり前と言えば当たり前なのだが・・・
そこで改めてブラックショールズモデルとはどんなものなのかということをざっくりでいいので勉強し直してみたのでとりあえずまとめておこう

まず前提として知っておかなければいけない用語がある。投資をやっている人ならだれでもよく聞いているに違いないがどれくらいの人が本当に理解しているのか

ブラウン運動
幾何ブラウン運動
ランダムウォーク
対数
正規分布
対数正規分布
算術平均
幾何平均
ボラティリティ

分かるような分からないような、分かったような気をして使っている言葉が並んでいる
言葉の定義というか実感として分かっておらず上っ面だけを知った気になっているため結局本質が何も分かっていない

ファイナンスでよくある勘違いミスリード

株価はランダムウォークしている、などと言われるがこれは実はミスリードであることを知った
ランダムウォークもブラウン運動も根っこにある考え方は同じであることを知った
株価はゼロ以下にはならないので対数正規分布である、というのも誤解を生みやすいということを知った
株価は対数正規分布だから幾何ブラウン運動であるというのも正確な表現ではないということを知った
ボラティリティが高いほうが最頻値や中央値が低くなりリスクが高いという場合平均値が同じだからそう言えることを知った
S&Pなどの指数を幾何ブラウン運動で計算すると元本割れする確率は5割以上になることはまずないが（ボラが低い場合）期待値がプラスだから当たり前の話だと知った

株価は正規分布していないというミスリード

ブラックショールズモデルでは株価が正規分布していることを前提にしているが、ここで言う株価とは要するに騰落率であろう。数学的には対数というのだろうが、株価の対数が正規分布していると言われるとわけわかめになるのが数学的素養の無い人間である(笑)
しかし、正規分布というからには平均があるはずである。勿論平均ゼロ、ということもある。もうお気づきだろうが一般的にボラティリティが高い低いなどと言っているがこのとき平均＝期待値がいくらかなどということはあまり気にしない。日々の騰落率からボラティリティを計算してもその平均値がいくらかなどほとんど気にしない。それはその平均値が限りなくゼロに近い場合が多いからだろう。
しかし、これを長い期間で捉えると（例えば1年単位とか）数パーセントの平均値が観測されることもあるだろう。

株価はランダムウォークしているというミスリード

そもそも仮に株価はランダムウォークしている或いはブラウン運動でもいいがそう考えると上がるか下がるかは同じ確率となる。上下の確率が2分の1だとしても値幅はまったく同じとは言えない。この値幅の平均をとると結果としてほぼゼロになるとするなら最終的には株価はどんどん下落していくことになる。
例えば毎回1％上昇し下落するときは1％だとすると必ず資産は目減りすることになるが、そうならないのは上下の確率が半々ではないか、半々だとしても値幅が同一だからではないからだと言える。
ブラウン運動ではなく幾何ブラウン運動だとしても結論は同じである。

ボラティリティが高いとリスクが高いというミスリード

S&Pなどの長期間に渡って上昇している資産を幾何ブラウン運動でシミュレートして元本割れの確率が一定程度観測できるが、ボラティリティが高くなるとその確率はより高くなる。
もしも株価が正規分布している、いや株価の騰落率が正規分布しているとするなら本来は期間が長くなればなるほど元本割れの確率が高くなるはずだが、そうならないのは平均値が高い＝期待値が高いからである。

上下の確率が半々でも平均値が高ければ株価は上がる可能性が高い

しかし、元本割れのリスクもある。その元本割れのリスクを測れるものがボラティリティと言われている。ボラティリティが高くなると端っこ＝所謂テールが増大しリターンも大きくなるが損失も大きくなるからと言われることもあるがこれは正確ではないだろう。なぜなら同一銘柄で計測している場合は平均値が変わらず、平均値が変わらないとは要するに当該対象期間でのリターンそのものはボラが高かろうが低かろうが変わらないことになるからである。平均値は変わらないのに元本割れのリスクが増大するということは損失が増大するのではなくその確率が高くなると捉えた方がよい。なぜなら株価がゼロ以下にはならないからである。
一方利益リターンはどうかと言われると、儲かる確率が低くなるが、儲かる時のリターンがボラの低い時よりは多くなるが、全体のリターンが増えるわけではない

ブラックショールズモデルのロジック

ブラックショールズモデルは原資産の対数が正規分布をしていることを前提としてそれが時間と共にどれくらいの動きをするのかというのをブラウン運動を使って計算している
しかし、先にみたように騰落率の平均値は考慮されていないようである。また原資産の満期での分布も上下の確率は50％である。
仮に原資産の期待収益率が対象期間3％だっとすると幾何ブラウン運動で計算すれば新甫よりマイナスになる確率は低いはずである。もっとも日経平均など主要なオプションは概ね期間1か月程度なのでそれほどの誤差はないのだろうが

正規分布を前提としているからブラックショールズは使えないというミスリード

いずれにせよ、ある期間がわずかであればともかくとして、期間が長ければその期間の期初と期末の資産感覚を一定期間ごとに計測していくと正規分布のようにはならないはずである。もっともボラティリティをいくらにするのか？期間をどうするのか？などによっても違いがでるはずなので一概には言えないが、不思議な事に2004年から2018年の限月毎の騰落率を当該期間のボラティリティでまとめると正規分布に近い分布になるのである(笑)

考えてみれば当該期間の日経平均は下落相場と言ってよく、1か月ごとの平均騰落率は1％もない。計算期間が20日程度でかつ期待値がほぼゼロであれば幾何ブラウン運動とは言え正規分布と明確な差がでないのかもしれない。

株価はどう動くか？幾何ブラウン運動の株価変動モデルを説明します。

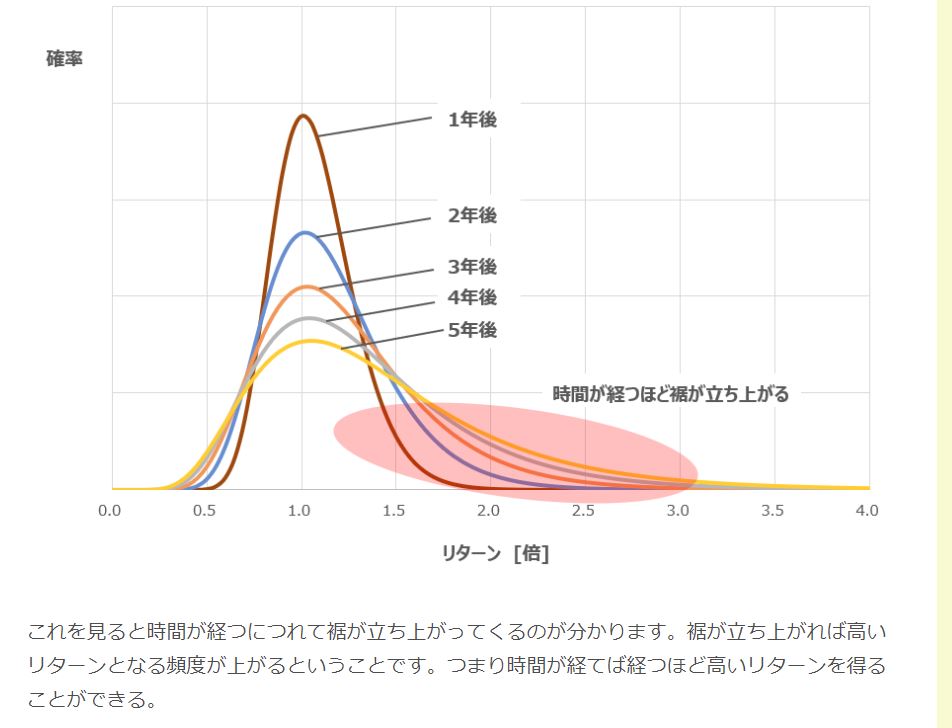
収益率7%・標準偏差20%での1年後は正規分布とあまり変わらないのがわかる

ということはやはりオプション価格を算出するロジックや構造から利益を掠め取るような手法を考えることはできない、ということになるのか？

例えばバイナリーオプションだと、各満期が3時間ごとで、13時から16時までの回だとザラ場引け後ナイトセッションが始まるまでの間はどうしても価格が停滞しやすいことが分かり、これをトレードに利用するのはやぶさかでない

オプションロングに限って言えばボラティリティが高いほうがよい

ボラティリティトレードというトレード手法があるが、ボラというよりIVが高くなった時にそのオプションをショートしてベガショート益をとりにいくなどはオプションをやっている人なら誰でもやっているだろう
このロジックからするとIVが低いときにロングして高くなったら決済するということになるが、先の幾何ブラウン運動をみるとボラティリティが高い場合はむしろオプションロングに大きなチャンスがありそうに見える
とは言え、IVが高くなれば低くなるという回帰性があるため、高くなったものを買うのではなく恒常的にIVの高い銘柄をチョイスしたほうがよいということになる。しかし、いずれにしろオプション価格はその想定IVで計算されるためその高いIVを織り込んだ価格ということになるので結局当該オプションを買い続けても儲からない(笑)
もっとも、幾何ブラウン運動の図を見るとわかるようにボラが高いほどよりテールが伸びる。全体のリターンは変わらない。仮に上下のリターンも変わらないとすると、幾何ブラウン運動ではマイナスの幅に限界があるため一回一回のマイナス幅が限定されることになりマイナスの回数が多くなる。他方プラス側は回数は少ないが一回一回のリターンの上限がより伸びるような感じになる
オプション価格は正規分布を前提としているので上下の確率は半々である。要するに全体のリターンを上下半々で割って価格を形成しているわけだが、そうすると前出の幾何ブラウン運動ではアウトのプットは無価値なものがあるにもかかわらずそこに価格がついていることになる。要はその権利行使価格のプットはショートで丸儲けだったわけである。
他方コールATMにしろアウトにしろ想定よりも多いリターンとなるが、それは1回でみた場合のはなしであって、結局はインする回数が少なくなりトータルリターンが変わらないという想定ならば買い続けても儲からないことになりそうである。しかし、それはATM付近のオプションにはそう言えてもアウトだとそうは言い切れない場合がある。
アウトのオプションは正規分布でも確率が少ない。例えばσ１以上の分布は約15％程度である。この付近の権利行使価格のオプションは15％程度のリターンがあることを織り込んだ価格設定ということである。
しかし、ボラティリティが高くなると、通常σ１以上の部分の上限値が伸びることになりこの部分の想定リターンが増大する。その反面ブラックショールズモデルではどんなにボラティリティが高くてもσ１のオプション価格の計算ではデルタ15である。
つまり、
幾何ブラウン運動でボラティリティが高くなると、正規分布では発生回数が多くなるATMより上付近の回数が減り、その減った部分が上昇方向のテール部分に追加されるイメージ
である。
とは言え、これはボラティリティが高くある程度の残存期間（恐らく1年以上）のオプションをずっと持ち続けて、かつ何度も試行して言えることであり、それを試しても必ずそうなるという保証はないしなんせ時間がかかりすぎて話にならない。そんなオプションを買い続けるくらいなら素直にその資産を保有したほうがいいかもしれない(笑)

ブラックショールズモデルではボラティリティ＝IVが高くなるとσ間の幅が広がるし、かつオプション価格も高くなるが、発生回数、割合は正規分布を仮定しての回数となる。
σ間の幅が広がると言っても権利行使価格の幅は変わらず、σ１の部分が上にずれる感じになる。

このようにみてくるとオプショントレードでの損益は多くの部分でボラティリティに依存していることがわかる。ボラが想定よりも高ければ儲かるし低ければ儲からない（ロングの場合）
ボラの高低が予想できればいいが、そもそも相場の上下が当てられないからオプションをやっているとも言えるのである(笑)

ブラックショールズモデルでのオプション価格というのはそれらをもとにして構築されているだけで別に将来を予想できるものでもない。原資産が満期の時点でいくらならオプション価格はこうなりますよという例示にすぎない。
株価がランダムウォークしているにせよしないにせよ、幾何ブラウン運動でボラティリティが高いとリスクが増大するにせよ、結局のところ相場が今後どうなるのかは分からない。分かっているのは相場は変動するということである。変動した結果満期時点で元の価格に戻っているかもしれないが、新甫から満期までずっと同じ価格であることはない。重要なのはその動く幅ということになる。

ボラが高かろうが低かろうが値動きは必ずある。またボラが仮に低いとしても値幅そのものは大きいこともありうる。ボラティリティとは平均値からどれだけバラついているかということなので、逆に言えばボラが高くても結果的に全く動いてないということもある。
従って、ボラティリティがどれくらいかよりもどれだけ上下の値幅をとれるだけとるといった戦略が儲ける一つの方法と言えそうである。
勿論値幅がどれくらいになるのかは分からないが、ボラティリティが高いほうが値幅は大きくなる傾向にあることは間違いないだろう。天底を当てることができれば話は早いがそうはいかないが、ボラティリティが高ければテールが伸びることは既にみたとおりだが、天井でコールを決済し、そこでプットをロングして底で決済するなどといった芸当は結局のところ出来ない。そんなことができるのであれば先物をトレードしてもいいわけでオプションをわざわざトレードする必要はない。
オプションを触るからにはそこにオプション特有のメリットがあるからであり、それを生かすようなトレードをすることで必然的にエッジがあるということになる。
ロンストを組めば上下どちらでも利益となりうるが、それができるには相場が一定程度以上どちらかに動く必要がある。

期中の動きを無視するブラックショールズモデル

この点ボラティリティが高ければ動く可能性は高くなるが、既にみたようにいかに大きく動こうがオプション価格はボラが高ければそれなりにそのボラが高いのを織り込んだ価格設定になっておりやり続けても儲からない。しかし、これはあくまで満期時点の話である。満期前の期間中では原資産が動けばオプション価格も動きそこで損益が発生する。
利益があがるにはできるだけ早くできるだけ大きく動くことであるが、それがいつ起こるのかそしてどれくらい大きく動くのかは分からない。とは言え、結局のところ大きく動けば動くほど利益はでるので動くほうに賭けるだけである。オプションは買い続けても売り続けても利益がでない、というのは満期まで保有した場合の話であって、期中においてはそれは分からない。
騰落率が正規分布を描くとは限らないので期中の例えば5日間だけの最大値幅がどれくらいになるのかは直近のボラからそれこそブラウン運動などである程度想定はできるだろうが、最高値、最安値が正規分布どおりになるとは言えず、正規分布どおりにならないのであれば儲けるチャンスがあるということになる。
ブラックショールズモデルはヨーロピアンオプションが前提でああるから期中の一定期間の値動き（ある時点からある時点までの期間で決済（そこを満期と考えることもできる））についてのリターンを織り込んだ価格設定ではないし、期中で決済ということはアウトのオプションでも価格がゼロにはならないので結局原資産の動きに対してのオプション価格の騰落率が損益となるので、元々のリターンを織り込んだオプション価格への依存度が満期まで持つよりも低くなるのは間違いない。特にＩＶが変わらず建てた時点から経過日数が短ければ短いほど元々のオプション価格はいくらであろうがほぼ関係なくなる。

そうすると、短期間で大きく動くと思えばロングをするのが王道といえる。もっとも、百発百中であたらないのが当たり前でいかに利益を伸ばして損失を軽減させるかということになる。

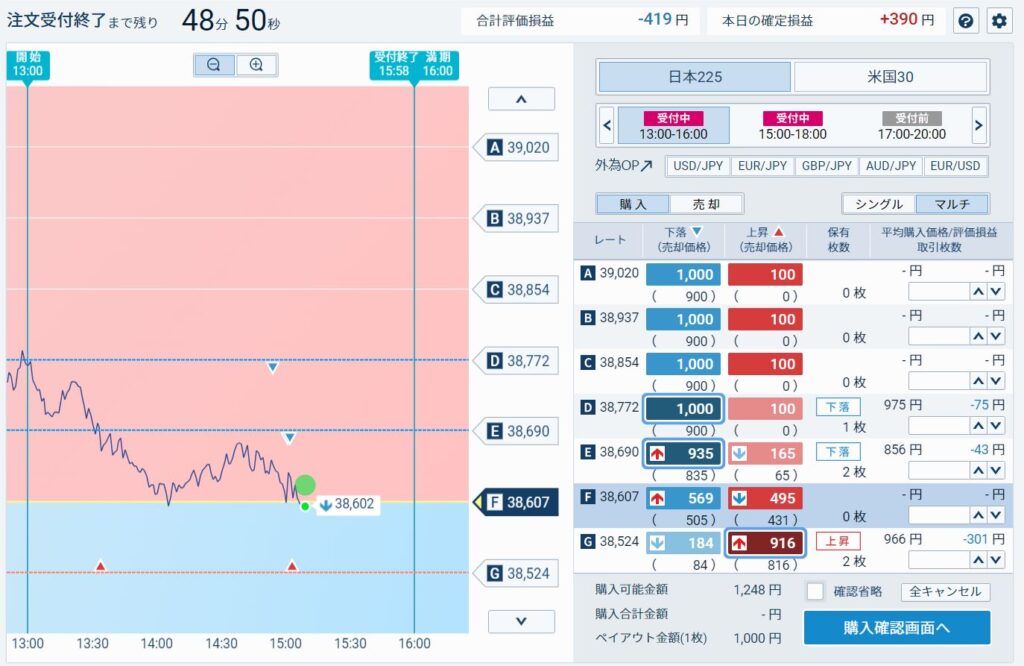
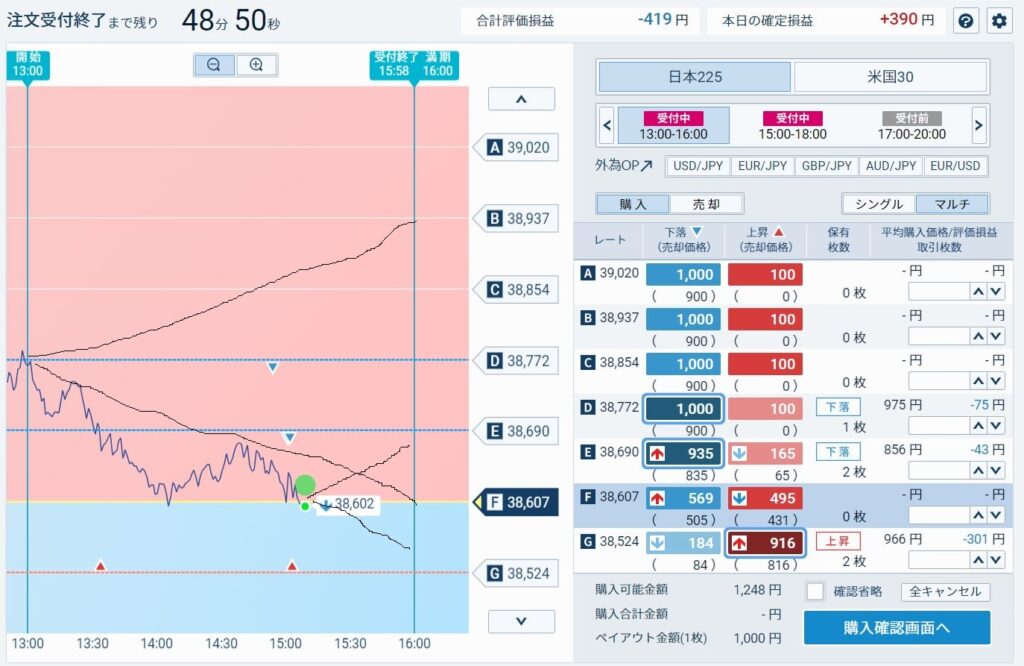
ある日のバイナリーオプションの動き
ATMがD38772から始まっている。期間は3時間で残り期間が3分の1に満たない。1か月満期の場合土日を除いて考えると大体1週間5営業日くらいの残存期間に該当するだろうか。
Fの38607ラインを-1σだと考えるとこれ以上下がる確率も少なそうである。また、ATM付近に戻るという確率は更に少ないと言える。
しかし、もともとATM付近から満期時点の価格の分布を正規分布で考えるならむしろATM付近に戻ってもなんの不思議もない。なんせブラックショールズモデルでは期中の価格は関係ないからである。
この事は幾何ブラウン運動で株価の変動を測る場合にも同じことが言える。要は計測開始地点から計測終了時点にいくらになるのかが問われているから期中においての価格は無視されている。
しかし、期中においてそこを起点にして残存期間までの価格分布を考えると別の景色が見えてくるわけでこのことにどう整合性をもたせた回答を提示することができるのか。いや、これをどうトレードに活かすことができるのかということになる。

ランダムウォーク理論からは開始時点の株価はなんの関係もないので現時点での価格からの分布となる。しかし、大多数の人がチャートを見て、様々なテクニカルを使ったりしなが価格を想定して取引するものである。それは人によって何を重視して取引するかの違いがあるだけである。つまり株価は以前の株価とまったく関係性がないとは言えないはずである。
とは言え、長い期間でデータを集計すると不思議なことに騰落率は正規分布に近くなる。逆に言うと、ある期間を切り取ると正規分布には似ても似つかない分布となることも多い。本当に正規分布であるならある一定期間を切り取って正規分布に近くなるはずであるがそうはならないのが株価である。
要するに株価は長期間計測すると正規分布に近くなるために正規分布から外れた場合に全体として帳尻合わせをしていることになる。正規分布というのは実際はそういうものなのかもしれないが。
対象期間1回ごとの結果の集まりが正規分布に近くなるだけであるから、正規分布で言えば-1σに当たる結果が5回連続で起きてもなんら不思議はないし、ATM付近でまったく動かないことが続いてもおかしな話ではない。それこそランダムというやつだろう。その事は逆に言えば、まったく動かない相場はいつか帳尻合わせの如く動く相場が必ず訪れるということでもあるが、勿論それがいつ起こるのかはブラウン運動や正規分布からは多分何も分からないはずである（分かるならそれは株価を予測できるということになりランダムウォークそのものが否定されることになる）

正規分布は結果論

仮に株価などの金融資産の騰落が正規分布しているとしても、正規分布しているからと言って株価がいくらになるかを予想してピンポイントで当てることなどできないだろう。
オプション取引に限って言えば正規分布することを前提に取引しても結局儲からない（儲からないように価格計算されている）から、逆説的だが正規分布しないときに儲かると言える。
正規分布する、というのはその対象期間全体の話で合り、一定数のデータがないと意味をなさない。
また、例えばσ１のオプションを買って、それがインしなかったらそれは確率85％なのでもっともだと思うが、絶対にインしないわけではないしインしたらインしたでそれは確率15％以内の事が起きたというだけの話である。そのσ１のオプションを100回買い続けるとインする回数が概ね15回程度になる、かもしれないという話で合って、確率15％に収束するのが300回試行した後かもしれないし500回かもしれない。
つまりボラティリティや正規分布などで確率云々言うことにほとんど意味はない。しかし、オプションは正規分布を前提にしているなら正規分布にならないときにこそ儲かるとも言える。
正規分布で言えば上がるか下がるかは半々だが、上がった後に必ず下がるわけではない。大体以前の株価とは関係なく動くというブラウン運動あるいはランダムウォーク的考えからすればやはり連続して上がったら次は下がる確率のほうが多くなるとも言える。

なぜ逆張りよりトレンドフォローが儲けやすいのか

いずれにしろ、回数を重ねていくと上下半々くらいになっていくが、必ず上がって下がるわけではなくむしろ上がって上がって上がってを繰り返す期間があると考えるのが自然である。
上がった後に下がるほうにベットするよりもむしろ上がって上がってにベットしたほうが利益があげやすいとも言える。
言い換えると正規分布だとこれからこうなりそうと考えてベットするにはある程度長期的にみなければならず、より短期目線では正規分布どおりにはならないと想定したほうが当たる確率は別として利が伸びやすいと言える。
逆張りよりもトレンドフォローのほうが儲けやすい、などと言った相場の格言めいたものがあるが、なぜそうなるのか数学的根拠はこのあたりにあるのかもしれない。

 

日経平均の上昇日下落日の平均

 

 

2004～2018

プラス平均　0.9961％
標準偏差　0.9707

マイナス平均　-1.055％
標準偏差　1.168％

	マイナス	プラス
σ１	1191	1156	0.32	0.31
σ２	388	538	0.11	0.15
σ３	115	161	0.03	0.04
	63	68	0.02	0.02
3680	1757	1923	0.48	0.52

 

ざっくりと正規分布っぽくなっているが、もとより正規分布ではない。上昇日下落日別にカウントしているので、上昇日にマイナスが発生することはないし下落日にプラスが発生することもない。また、正規分布は本来平均値にσを±してどのような分布になるかをみるものであり、この集計方法は平均値関係ないのでもはや正規分布とは何の関係もない。

年によってそれはより顕著にあらわれる。

 

2023

 

プラス平均　0.7829％
標準偏差　0.614

マイナス平均　-0.836％
標準偏差　0.6245％

 

	マイナス	プラス
σ１	49	68	0.20	0.28
σ２	25	42	0.10	0.17
σ３	22	22	0.09	0.09
	7	10	0.03	0.04
245	103	142	0.42	0.58