- 投稿 2024/12/29
- 未分類
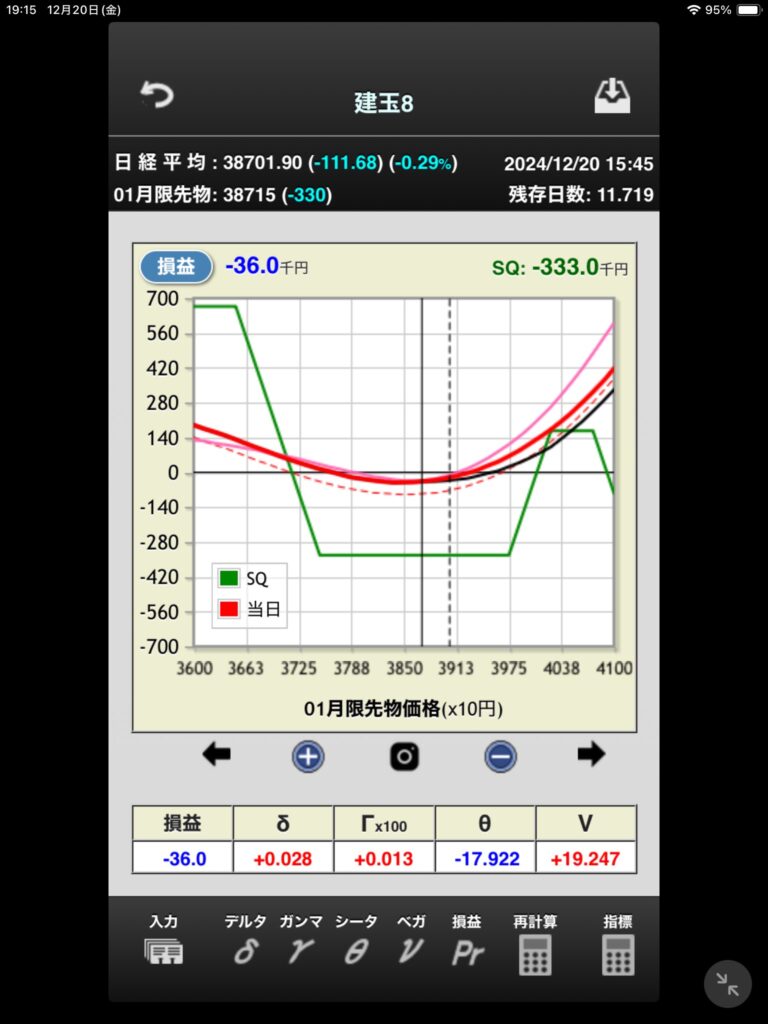
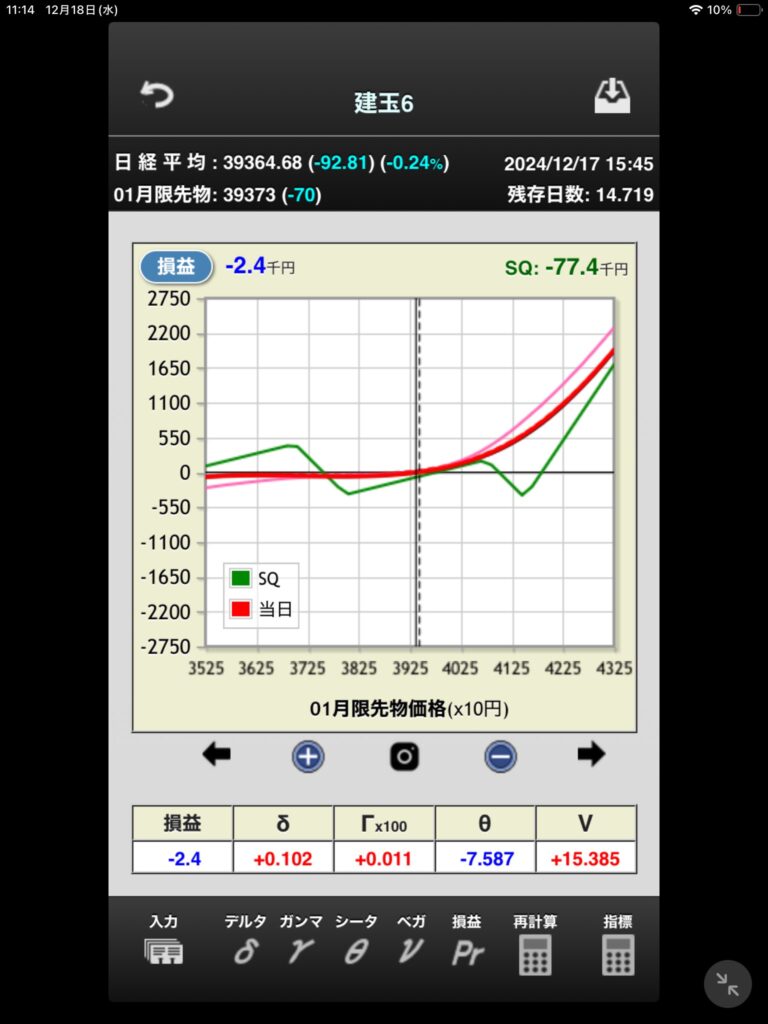
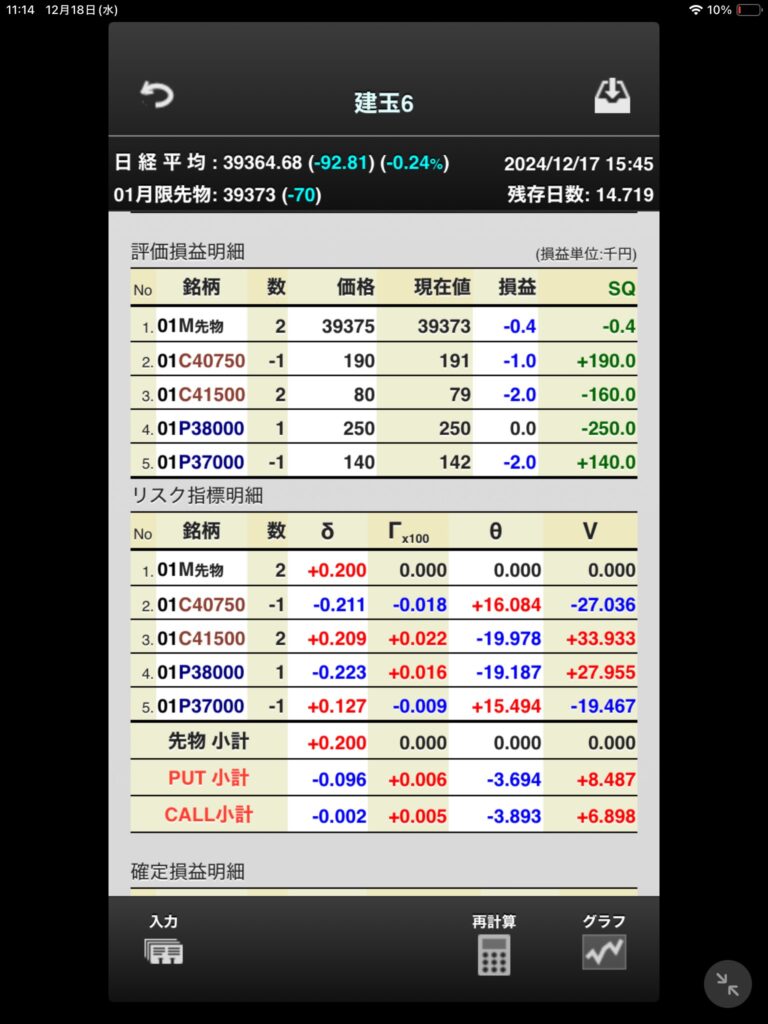
デルタヘッジ戦略はIVと実現ボラの差分
端的に言えば実際のボラティリティより高いIVのオプションを売却し、適切なデルタヘッジを行うとその差分が儲かるといことになる。
従って巷間よく目にする先物売りのコール買いによるデルタヘッジ戦略では本来実現ボラより低いIVのコールを買って利益をあげることになるが、一般的な説明は相場が上昇したときにヘッジで先物を売り、下がったら先物を買い戻すことで利益をあげる、などと説明されている。この考え方だとIVは特に関係なく、とにかく相場が上下してくれないと話にならないし、実際その上下の回数が多ければ多いほど利益になる、などと説明している記事も多い。しかし、この場合購入したコールは恐ろしく減価していることは想像に難くない。先物売買では利益がでても肝心のコールがクズ化していたらお話にならないがその点はスルーされていることが多い。これはデルタヘッジの本質をよく分かっていないからだろう。いや、デルタヘッジというよりはデルタヘッジで利益をあげるという意味がよく分かっていないと言ったほうがいいだろう。
一方でデルタヘッジで利益をあげる場合の利益の源泉はIVと実現ボラの差と言え、オプションを売却する場合のデルタヘッジ戦略では実現ボラが高くなると損失となるため必ず利益のあがる戦略ではない。
実際の取引において実現ボラティリティが正確に予測できるなら必ずしもデルタヘッジに拘る必要はないとも言える。
他方で、この戦略理論は満期まで持つという事が前提になっている。例えば残存期間20日のオプションを売却する場合にIVのほうが現実のボラより高いと想定し売却したとして適切にデルタヘッジを行っても、日経平均のSQのやり方だと、取引最終日との間にタイムラグがあるため価格がとんでしまうことがあるので適切にデルタヘッジができずに満期持ち越しになってしまう可能性が高い。従って事実上取引最終日までには決済することが現実的となる。そうすると、最終的な満期時点のボラティリティではなくなるが、あまり大差はないとも言えるが、結局のところ満期まで必ずしも持つ必要はなく、ある時点で有利な状況になればそれで決済することで利益があげられるならそこで決済してもよいはずである。
有利な状況があらわれず、満期前まで持ち越さざるを得なかったとしても結局それは同じことだし、仮に期中でかなり有利な状況になったとしても満期まで待っていたら不利な状態に陥ったということもありうる。
そもそも、デルタヘッジはなんのために行うかと言えば価格変動リスクをなくすためだと言われる。価格の変動リスクがなくなれば確かに損失もなくなるかもしれないが、完璧なフルヘッジだといくら価格が上昇しようが利益もないことになる。そんなものはやる意味がない。
また、オプションの場合はオプションを売却する場合と購入する場合でそのリスクを考えた時、売却する場合のほうがリスクが大きい。ここで言うリスクは確率ではなく、損失の増大という意味である。
その意味ではヘッジを行うことに意味はあるが、オプションを購入する場合にわざわざヘッジをする意味があるのかという疑問がある。
オプションを購入する場合のリスクはその購入金額に限定されているし、まだ実現されていない原資産のリターンを前もって支払うというコストを払っている。価格変動をしなければほぼ利益はでないと言ってもいい代物に敢えて本来のヘッジという意味でヘッジを入れる必要はないとも言える。
デルタヘッジ戦略ではIVと実現ボラの差が利益の源泉となるが、満期まで持たずに決済することを考えると必ずしもそうはならない。実際のボラティリティはむしろ関係なく、IVがどうなるかである。
また、売却した時点よりもIVが高くなったからと言って必ずしも損失になるとも言えない。
例えばコールを売却して先物を購入してデルタヘッジを行った場合、相場が下落するに伴い先物を損切りしていくことになるが、相場が下がり続けるとIVが高くなることが多い。通常はIVが高くなりコールの価格があまり下がらず、先物損切り及び含み損のほうが上回る場合が多いが、これも時間が一定程度経過している場合は十分利益になる場合もある。
このように考えていくと、デルタヘッジはそもそも必要なのか?という疑問が湧くのも道理である。少なくともオプションを購入する場合はヘッジの意味でのデルタヘッジは必ずしも必要ではない。
他方、オプションを売却する場合のデルタヘッジはヘッジという意味ではやる意味があるが、ヘッジという意味ならば適時にデルタヘッジを行う必要はないとも言える。
オプションを売却した場合のリスクは結局当該権利行使価格にインした場合の話であるので、インする場合に限ってデルタヘッジでリスクを回避すればいいということになるし、オプションを売却した時にプレミアム分は得ているので、その価格分インした時にデルタヘッジを行うということでも問題ないことになる。
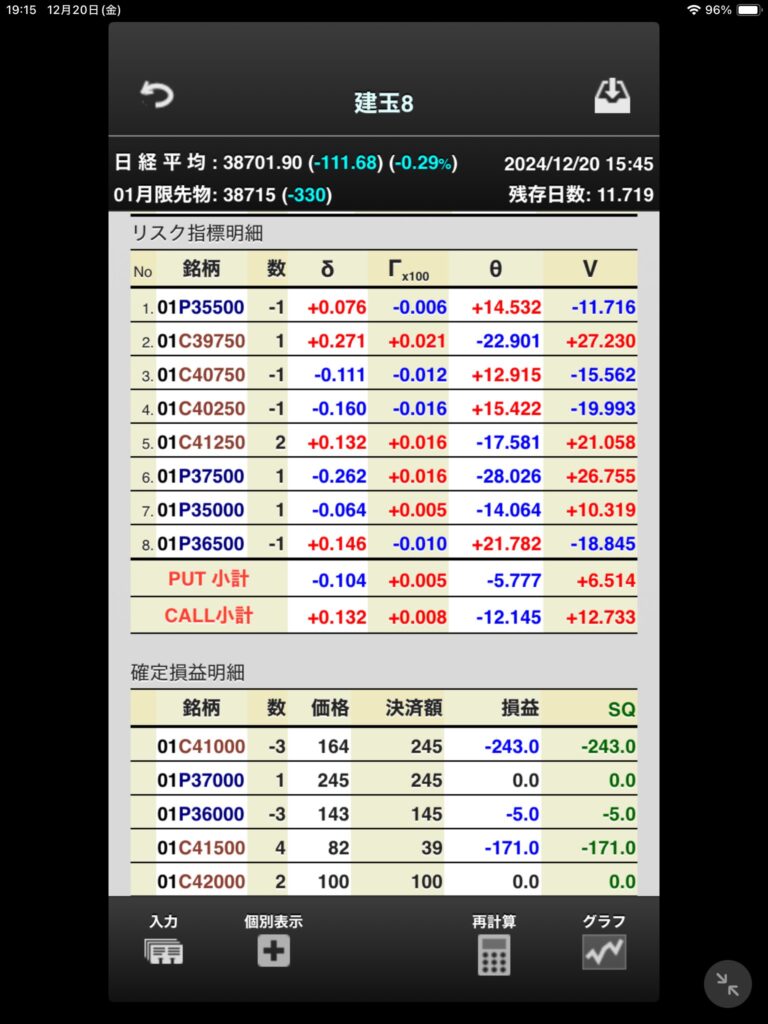
デルタヘッジによってベガとセータとガンマが残る
別の見方をするとデルタをヘッジすると、いわゆるギリシャ指標と言われるもののうち代表的な3つが残る。
このうち既にみたようにIVの上下がデルタヘッジで重要であり、これは要するにベガがリスクとして残っているからである。オプションを売却するときはマイナスのベガであり、IVが上昇すれば当然不利となる。
この時、セータはプラスなので時間が経過すればするほど有利になるというわけである。
ガンマはマイナスなので不利となるが、このように見てくるとオプション取引というのはこれらのリスク指標の何を取って利益をあげようとするかと言い換えることができる。
デルタが相殺されてゼロであってもコールとプットをともに売却しいる場合は必ずしも価格変動リスクがないとは言えないのは、ガンマがマイナスだからである。その反面セータは大きくプラスになっているし、逆にベガは大きくマイナスだろう。