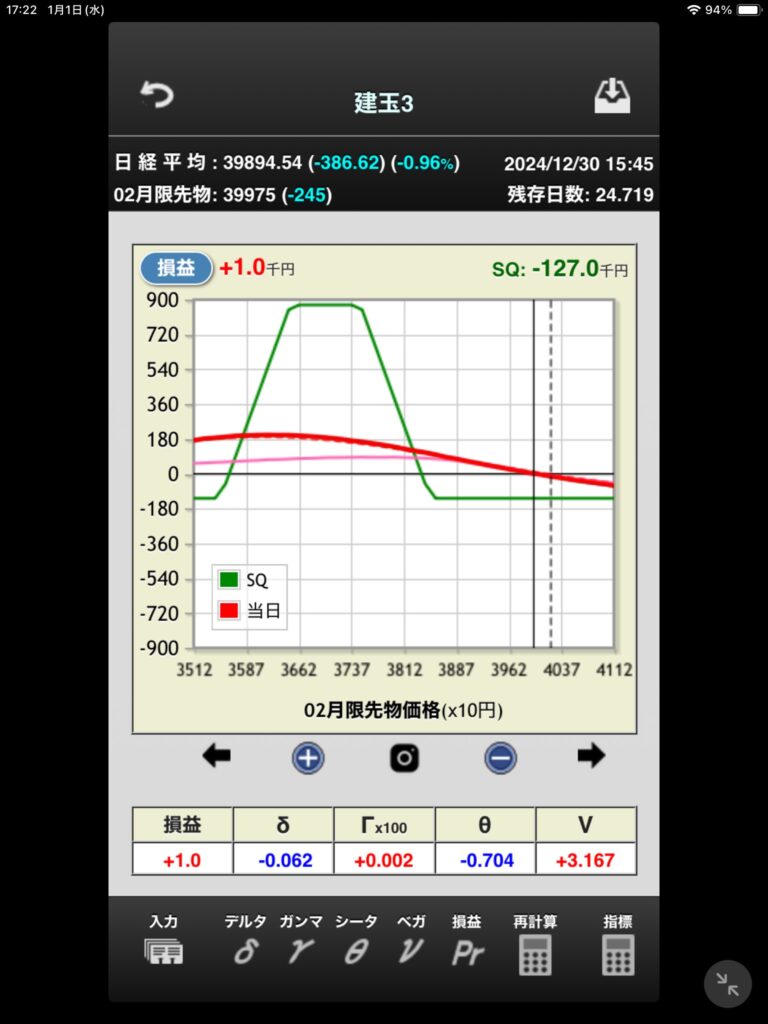
- 投稿
- 日経225オプション - 未分類
ふと思う。ボラティリティ=標準偏差とは平均からどれくらいバラついているか?という事を表すものだとされている。
つーことはだ、例えば平均がかりに1%の場合だろうが4%だろうが、マイナス10%だろうが、そんなことは実はどうでもよく、その平均とやらからどれだけ逸脱するかを見るもののはずである。
そうすると、オプション取引においては満期時点で毎回毎回常に平均のプラス4%の上昇をしたとしてもそれはまったく意味がないことになる。なぜなら満期時点のリターンが織り込まれた価格設定がなされているからである。要するにその平均値からどれくらい大きく逸脱するかにオプションの損益が左右されることになりはしないか。
だとすると、やはり満期時点まで待つ必要はなく、想定平均値を上回るような騰落を示した時に決済=利確することが望ましいということになりはしないだろうか。。。
とは言え、騰落には±があるのでそれを単純に合算してしまうと平均値がプラマイゼロ近辺に収束してしまう。
そこで、上昇する場合と下落する場合に分けて考える。例えば上昇する場合に限っての平均値がプラス1%だとする。そうすると、仮に1.8%の上昇をしたとするとそれは平均値を大きく逸脱していることになる。
もっとも、それを時間足単位とか1日単位の騰落で考えるとやりにくい。平均値を大きく逸脱することがそう頻繁に起こるわけではないし、起こったとしてもその前に下落していればコールを買っていたとしてかなり減価するはずで、その後2%上昇しても購入価格以下になっているかもしれないからである。
そうすると、いずれにしろ少なくとも数日はそのチャンスをうかがうためにポジションを保有する必要があり、また、必ず上下の予想が当たるわけでもないことを考慮すると、両建て状態いわゆるロンストのようなポジションを持ち、利確ポイントは数日間の上下別の平均値を逸脱した場合になりそうである。
例えば10営業日の上昇平均が3%だとすると建てた時点の原資産の価格から3%以上上昇したらコールは利確しなければならない。両建てをしている場合はプットが損切りとなり、ここでトータルプラスになるか?という話になってくる。当然ながら期間が長引けば長引くほど不利に働き、IVも下落すると不利になるためどこかで損切り、もしくは撤収する必要が出てくるかもしれない。
例えば1%上昇したが、その後3日かけてそこから3%下落し、その後翌日に1%戻すとすると、5日かけて原資産がマイナス1%となる。この場合はプット側も利確ポイントに到達せず(原資産はポジション構築時から2%しか下落していないため)、ポジションは保有したままでセータ分は確実に減価しているだろうし、IVも下落しているかもしれない。そうすると少なくともコール側はかなり減価していることが考えられる。
結論からいえば両建てにしていると3%程度の騰落では利益が出ない。時間がかかればかかるほどそうなってしまう。