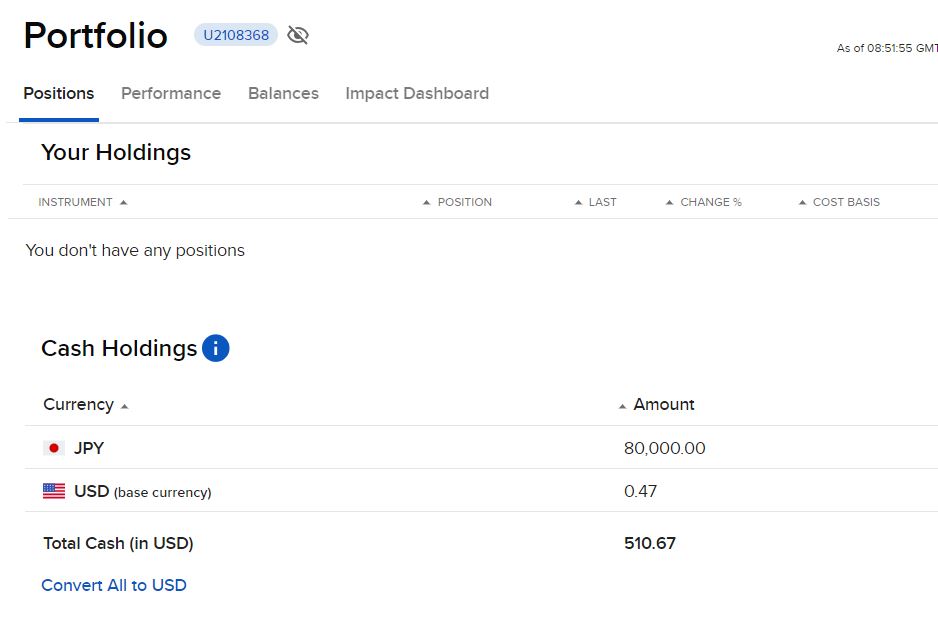
ビットコインのETFが上場承認されたというニュースから少し経つけどビットコインだいぶ下がってきましたね。
ビットコインのコールオプションでも買おうか。ビットコイン自体既にオプションが取引されてはいるけどどうせならETFのオプションがいいということで
色々あるようなので少し検索を
先物ETFと現物ETF
bito
BITO はビットコイン先物に投資しており、ビットコイン自体には投資していません。このファンドがビットコインの収益を厳密に追跡するという保証はありません。
なるほど。これは先物対象か。考えてみたら先物と現物がどれくらい連動しているかとか、先物コンタンゴで買い続けたら結局減価して儲からないとかあったら意味ないやんけ(笑)
やっぱりなんでも自分で調べてみないとだめだと改めて痛感。
どうやらこのETFが現物ではもっともでかいようだ。
ibit
しかしオプションがない・・・
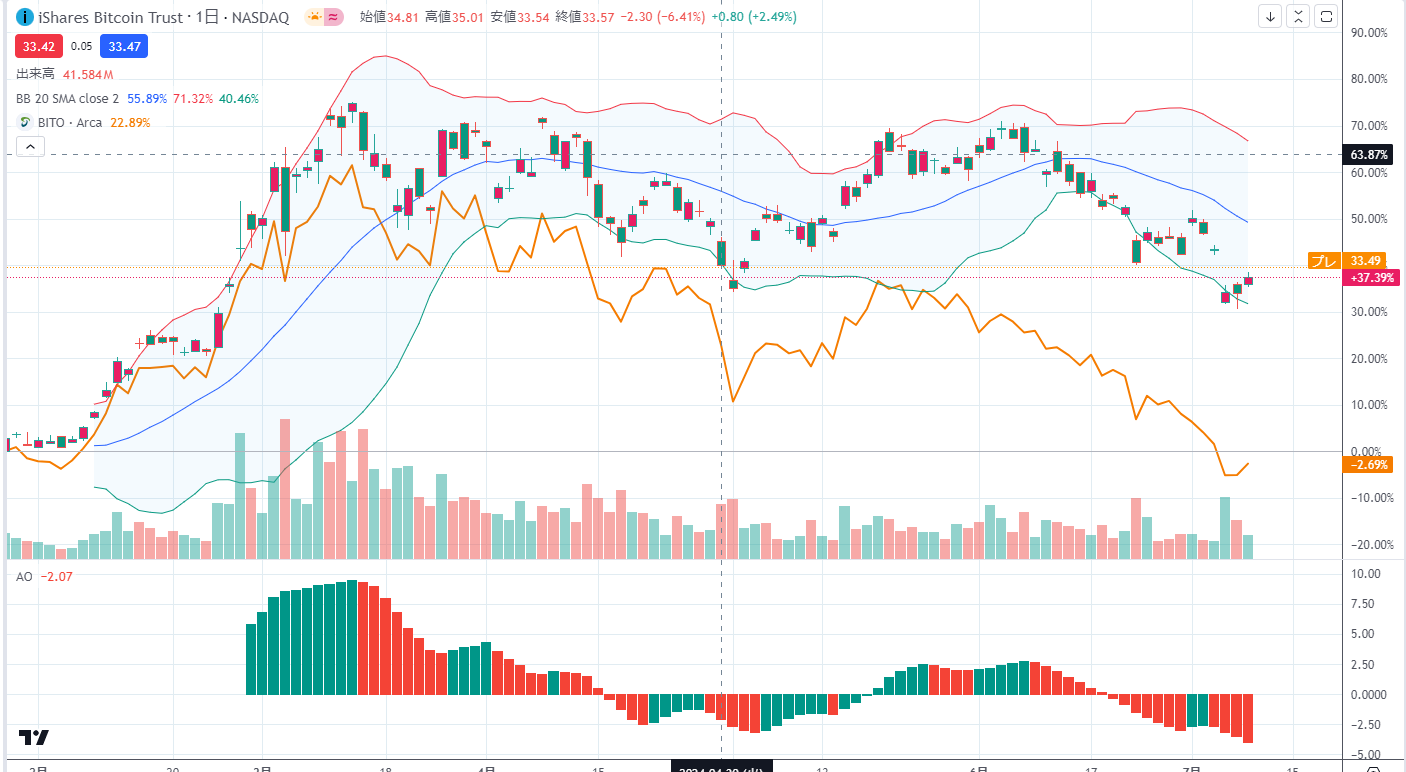
先物コンタンゴの減価
やっぱり先物ETFは現物ETFとくらべて価格が乖離しているな。先物はコンタンゴということかしら。
とは言え、先物って取引所によって違ってくるはずだと思うが価格自体はサヤ寄せするから気にしなくてもいいか。
いずれにしろ基幹構造が問題だな。やはりコンタンゴのようだ。商品先物と違って、ビットコイン自体を保有するのにそんなにコストもかからないだろうし、先物自体は差金決済されるみたいだけど期先のほうが高くなるのはVIXに似ている。
ビットコイン先物とは?
ブロックチェーン株式とビットコイン先物取引を支持する理由
>ビットコイン先物取引は差金決済される商品です。契約期日に、ビットコイン先物取引はビットコインの直物価格に収束するものと予測されていますが、この収束価格が上昇したか下落したかによって、現金の支払が買い手から売り手に対して行われるのか、またはその逆となるのかが決まります。
>ビットコイン先物取引は、伝統的にコンタンゴの状態で取引されてきました。つまり、期間が長ければ長いほど、直物価格より高く取引されてきたということです。このようなビットコイン先物取引の動きは、概ね2つの主要因によるものです。1つは、先物取引を通して得られるレバレッジのかかったエクスポージャーに対する需要です。もう1つは、ビットコイン直物をビットコイン先物取引(ショート・ポジション)の証拠金にできないことです。つまり、先物ポジションとビットコインそのものの裁定取引は資金効率が悪いということです。
>2021年10月において、期近先物取引のロール取引を1年間行った場合のリターンは325%となりますが、これは直物ビットコインの361%に対してアンダーパフォームしています。これは先物取引において、この期間中に発生するロール・コストによるものです。
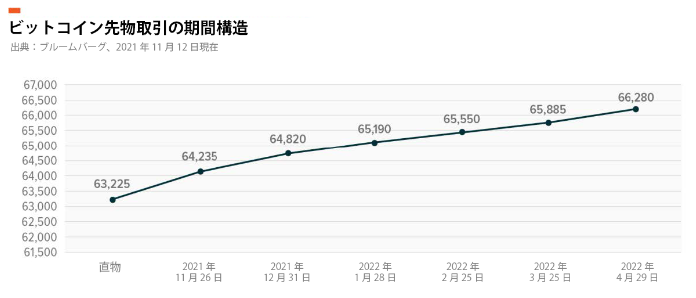
1か月あたり3%減価する。言い換えれば先物価格は新甫で3%高いということか。
とは言え、現物ETFは今年の2月から3割程度上昇しているのに先物ETFはほぼ変わらずむしろマイ。1か月あたり5%と高くなってるじゃないか。ちょ待てよ、そもそも現物ETFは現物の値動きと正確に連動しているのか?
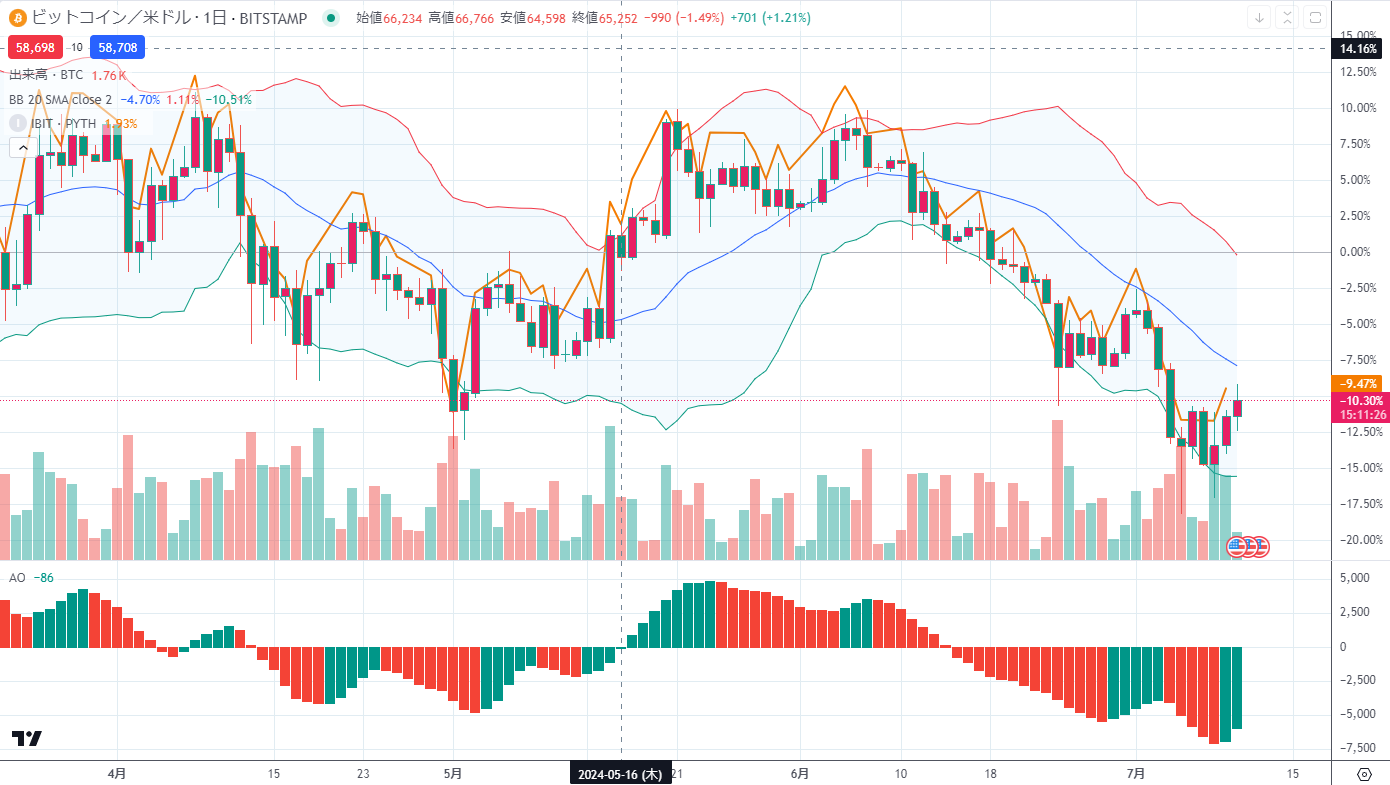
現物買い先物売りでサヤが抜けるのか
連動していると言っていいようだ。ん?ちょ待てよ!
これってビットコイン現物買って保有して先物売っとけば労せずして裁定取引の完成ではないか(笑)かつてロスチャイルド銅のサヤ取りで儲けたのと同じ。
現物買わずともETFを買い保有して、先物ETFのオプションでプット買いコール売りの合成先物売りでよかろうもん
プロが解説:ビットコイン現物と先物を利用して「安定して利回りを得る」運用手法
そりゃそうだよね。しかし、この記事によると先物が高いのは金利+ポジションの偏り(ロング)ということになる。
先物の満期日は最終金曜日なので今月あと残日数15日
7@58965
8@59540 @7+0.975%
9@59950 @8+0.688%
現物は58425前後なので7月限は約+0.924
思ったほどサヤは開いていない
6/28 現物60230程度 7月限 61020程度なので約1.3%程度高く始まっている。にしても先物ETFのBITOは乖離しすぎじゃないかな
しかし、こんな記事を発見
ビットコイン先物ETFは現物価格とほぼ一致、ロールコストの懸念は杞憂:プロシェアーズ
>「上場以来(7/18まで)、ビットコインのリターンは-51.5%で、BITOは-54.5%だ。そして、そのささやかな差の半分以上は、BITOの年率0.95%の手数料だ」。
>ハイマン氏によると、BITOはファンドの保有する現金による金利収入が、アメリカ経済の金利水準に密接に連動するロールコストを補っているため、スポット価格に密接に連動し続けている。
>「CMEのビットコイン先物のように、保管コストのない金融先物では、先物契約プレミアムは期間相当金利と同程度になるはずだ。2022年3月以降、連邦準備制度理事会(FRB)が基準金利を5%引き上げたことが、こうしたプレミアム、ひいてはビットコイン先物戦略のロールコストを押し上げる主要因になっている」
この記事が書かれたのは2023年 7月 22日
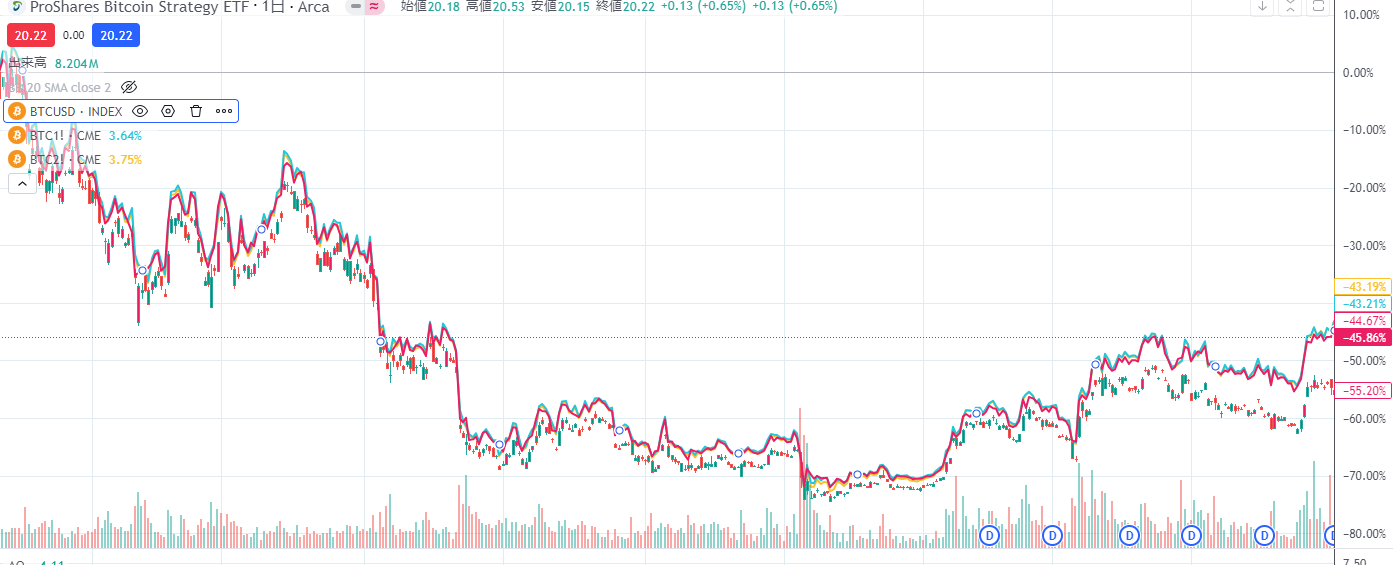
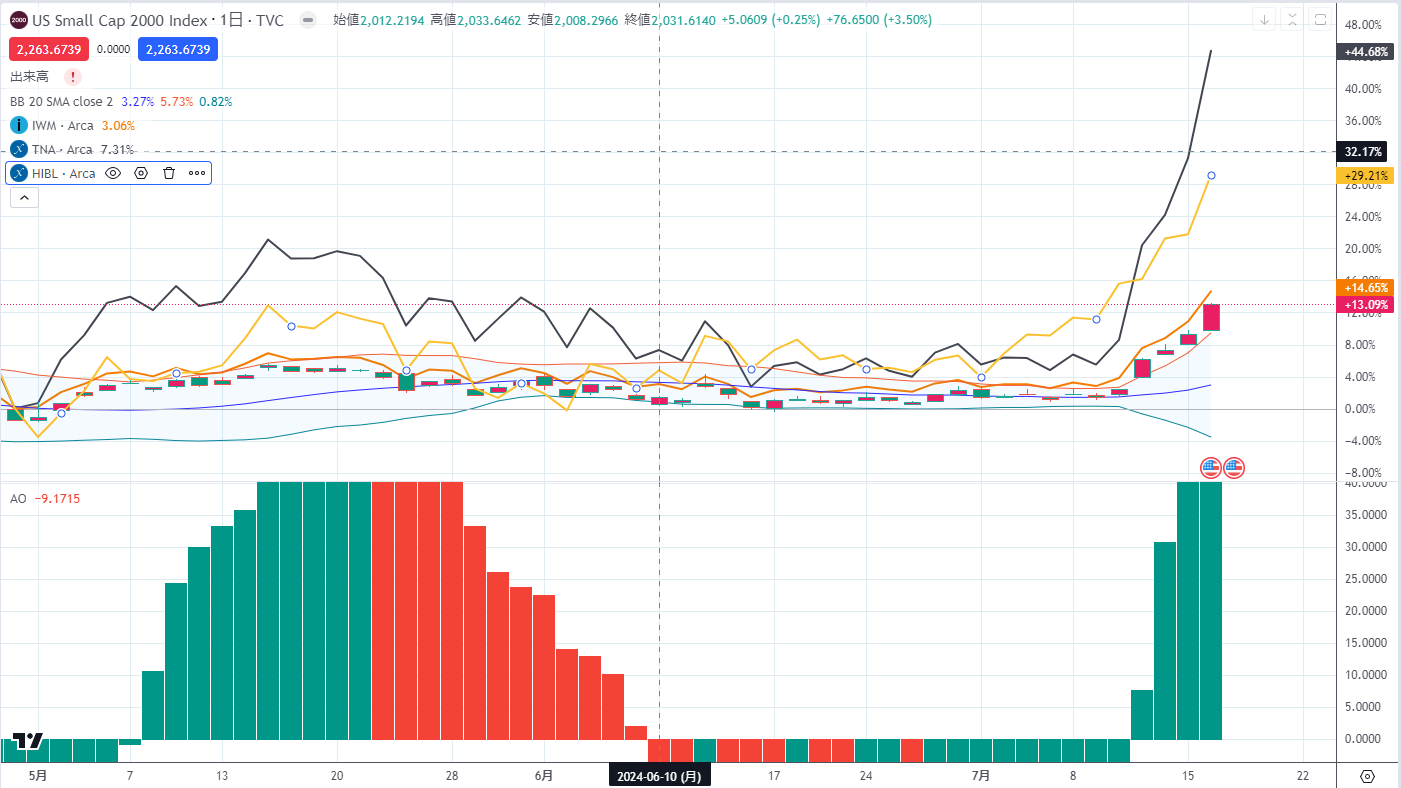
同期間をざっくりとトレーディングビューで比較表示してみると現物比約10%程度の乖離がある。金利収入を配当で支払っているとするとこんなものか。
もしかすると先物価格自体があまりコンタンゴになっていないのかもしれないと思い、先物も表示させたが恐らくつなぎ足のせいか現物とほぼ同じになってしまう
>アメリカ経済の金利水準に密接に連動するロールコストを補っているため、スポット価格に密接に連動し続けている
だとすると、金利以上に限月間にサヤが開いていればサヤが抜けることになるがそもそもこのETFは先物をどれくらい保有しているのか

なるほど、先物指数みたいなやつがあるのか。つーことはその指数がどんなロジックで先物をロールしたりしているのかみる必要があるな。めんどくさい(笑)
これか?
ビットコイン先物 - 契約仕様
んでこの中の決済手続きだな?
CME ビットコイン先物日次決済手順

>ティア 1: リード月と 2 番目の月のスプレッドが Globex で 14:59:00 から 15:00:00 CT の間に取引される場合、スプレッド VWAP が計算され、スプレッドの最も近い取引可能なティックに丸められ、リード月の決済に適用されて 2 番目の月の決済が導出されます。
期近の先物価格(厳密にはその日のVWAP)に期先ー期近のスプレッド(厳密にはそのVWAP)分を加減するのが基本のようだ。確かVIX指数だと先物が日々徐々に入れ替わっていくような感じだったと思うがやっていることというか考え方自体は同じようなものなのか?
通常のロールオーバーで、先物コンタンゴだと端的に期近を売却し高い先物を買い直すから、この時CFDなどは価格を減算する(価格調整額の支払いになる)
VIXなどの先物ETFの場合は日々期近を30分の1売って期先を30分の1買う、みたいなことを計算上行う(多分今はやり方が変わっていると思うが)ので、この場合は現物価格が変わらない場合でも期近は元々高く買っているので満期に向けて先物価格は下落していき売却損が積みあがっていく。現物価格が上がればその分期先の価格も上がっているのでロールしても結局同じことの繰り返しになる。
一方でCMEのビットコイン先物指数(と言っていいのか)はどうか?
期近の価格を一応ベースとし、そこにスプレッド分を加味するわけだが、この場合期先が高い場合は減算するのか加算するのか?理屈で言えば期近から期先に乗り換えるわけだから価格そのものは上がる。ロールする場合は期近を売却し、そこで一旦清算されるのでそれが減価につながったりするわけだがBITOの場合は常に期近を保有し続けることになる。
満期になり、期近から期先に交代した場合も当然スプレッド分が加味される。期先が高いコンタンゴ状態でもスプレッド分が常にプラスされると結局期近先物と現物価格の価格差に収束し、おおむね先物価格が高いのでその分は減価する。勿論スプレッド開いたり、ときには逆ザヤ=バックワーデーションになったりすることもあるが
先物コンタンゴで減価していくものを説明するとき一般的には限月間の価格差みたいに言われることが多いが、実際は期近の先物をいくらで買っていくらで売却したかという部分がキモなので確かにこのやり方はむしろ理に適っているののかもしれない
さすが金融大国アメリカである(笑)
そして、注意しなければならないのはその2023年7月から現在までの比較チャート
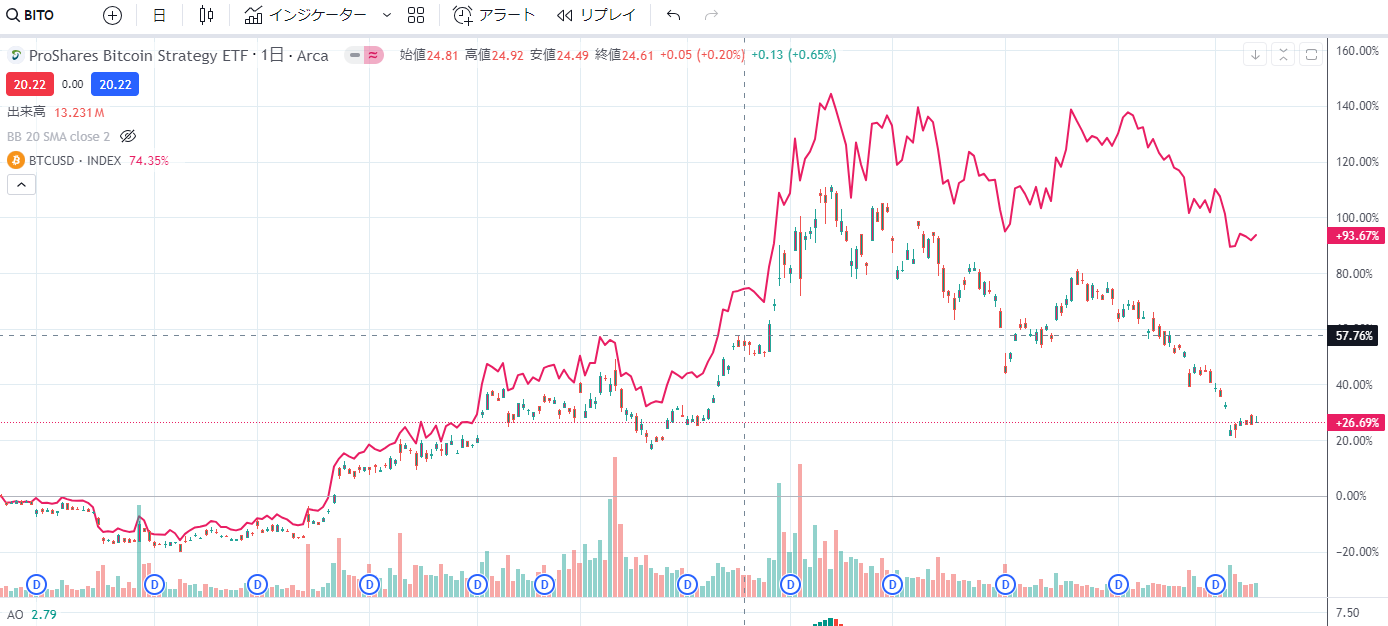
現物は+93%
BITOは+26%
圧倒的じゃないか(笑)
>アメリカ経済の金利水準に密接に連動するロールコストを補っているため、スポット価格に密接に連動し続けている
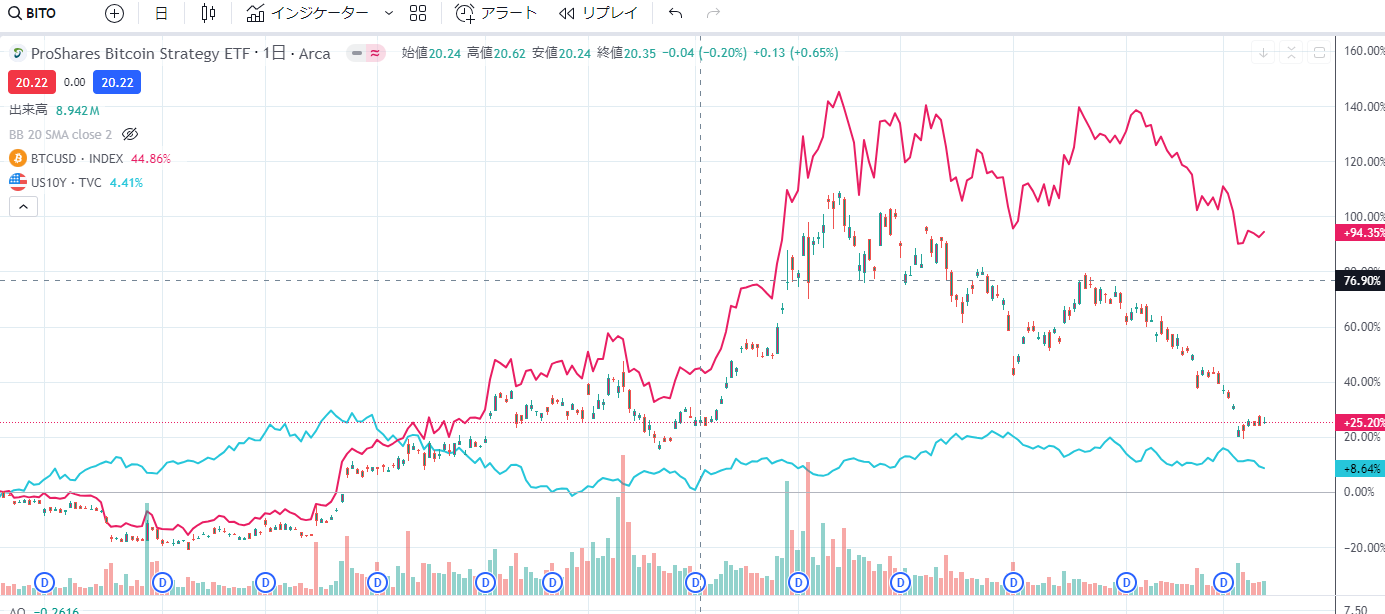
10年債の金利はほとんど上がっていないため上の言葉が正しいならロールコストを補えていないということになり、それは詰まる所ロールコストが存在しかつ、そのコストは先物価格が高いということになり、結果BITOだから現物価格に連動する、とは言えないということになるな
早速インタラクティブブローカーズでBITOのオプション価格を参照してみる
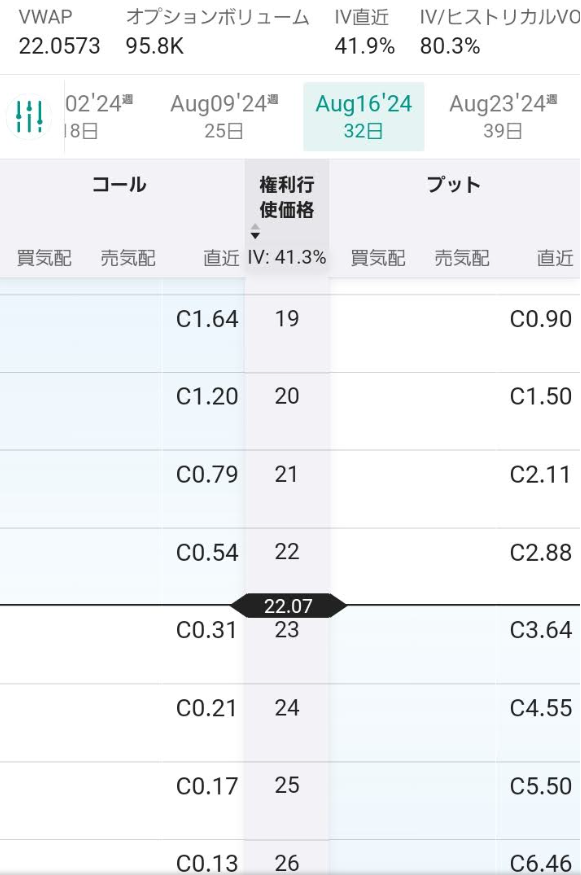
しかし、考えてみると価格そのものが違うので現物とBITOのサヤ取りといってもどれくらいの割合にすればいいのか難しいな(笑)
とは言え、その前にオプション価格に既に減価分織り込まれてるな・・・そりゃそうか
にしてもBITOの価格が20.2くらいに対して8月限のATM22
プット 2.88
コール 0.54
ってひどいな(笑)ちゃんと価格はついているのか?念のためfirstradeで確認するとやはり
仲値で
プット1.43
コール1.23
位になる。この価格だと現物が高ければ確実にサヤが抜ける。しかし、BITOそのものの現物はない(笑)現物のETFを疑似的に同じ価格相当買うってBITOの合成先物を売る、でいいのか?
現物に連動する(厳密には指数になるのかな)IBITがローンチされたのが今年.。かなり近い価格なのでまず比較してみよう
チャートだけでは見えてこない配当
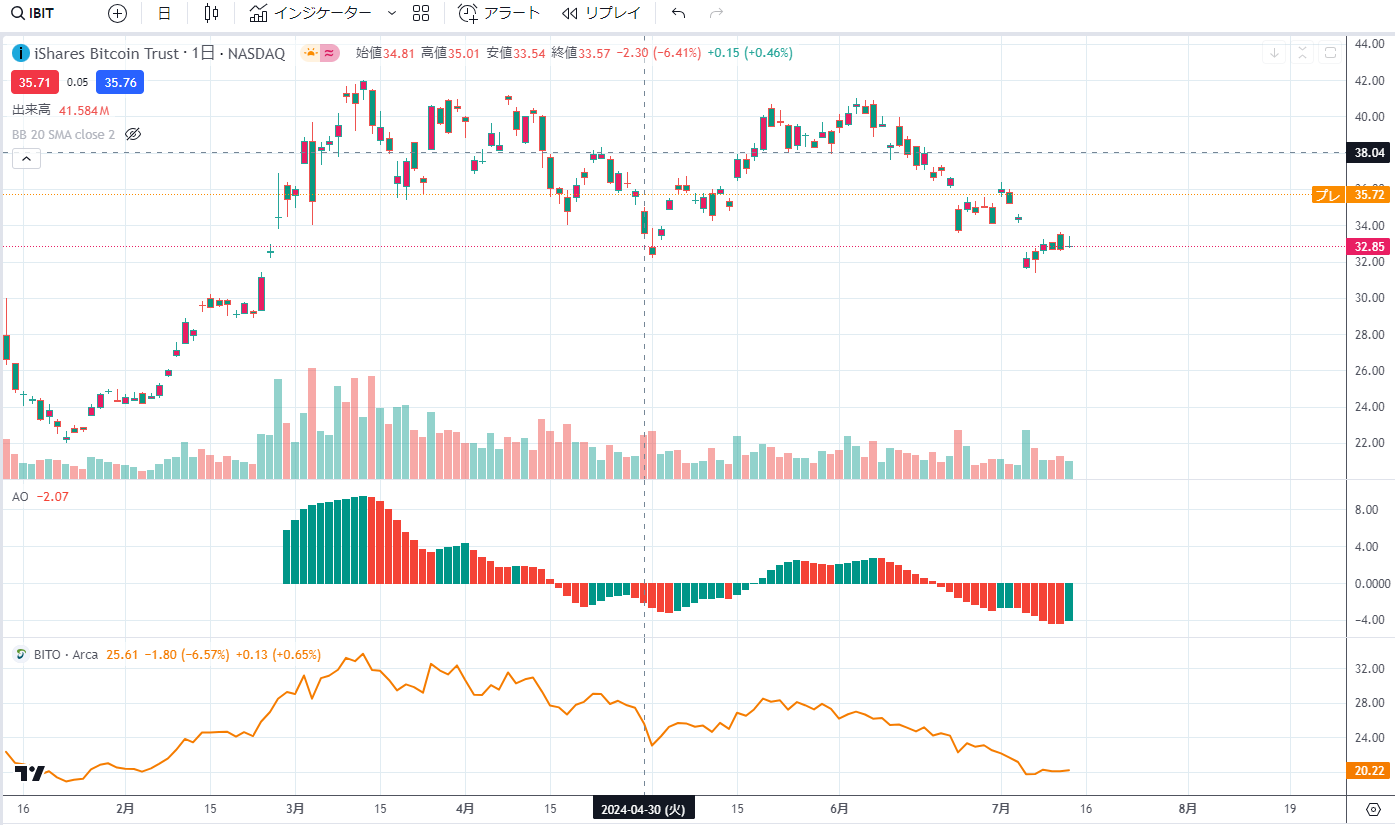
ibit bito
1/26 23.99 20.3
2/22 29.72 24.6 2/1 0.36
3/21 37.15 29.8 3/1 0.73
4/25 36.86 28.22 4/1 1.15
5/23 38.27 27.2 5/1 1.68
6/20 37.04 24.48 6/3 1.77
7/25 7/1 1.5
BITO のヒストリカルデータを見ると清算価格が無視できないほど大きいがこれは一体何なのか。それと配当もデカく毎月配当がある
先物を日々ロールする場合現物価格は直接関係ない
目論見書を読むと先物を買って売るみたいなことが書いてある。ん?先物非株式指数に投資するんじゃなかったのか?そもそもなぜ配当がこんなにブレているのか?
ファクトシートを見ると保有資産にしっかりと先物があるな・・・(笑)
どうやら先物指数みたいに書いてあるやつは先物のティッカーみたいなやつで、先物価格の日々の清算ルールみたいなやつのことを指数のルールだと勘違いしていたようだ(笑)
やってることは単純に先物をロールしているということでよさそうだ。コンタンゴだと減価する、というのは価格が上がらない場合のことであって、今年に入ってビットコイン価格が急騰したが、こういう時はいくらコンタンゴだろうが価格そのものは上がっていくのは間違いない。また、先物を買って売却するわけだから当該先物価格が上昇していればそこに利益が生まれるわけで、常に上がり続けているような場合は利益が蓄積される。VIX先物ETFの場合は圧倒的に価格が下落していることのほうが多いため見えづらいが、BITOの場合は利益が出た場合はそれを再投資するのではなく配当に回しているということのようだが、そうすると直近のほうが配当が高いな。。。(笑)
この点VIX先物はどうなっているのか?しかし、よくよく考えると、売却益が出た場合は配当に回していたら、売却損が出た場合は補填できず縮小していく。従って本来売却益は再投資すべきではないのかな。知らんけど(笑) これらのファンドはなぜ配当金を分配するのでしょうか?
そういえば日々の清算価格?調整価格はどういった意味あいなのか。直近の価格は終値と同一になっているのも何だかよく分からない。いずれにしろ市場で取引する場合は無視していいのか、な?
今年2月から7月の配当合計 7.19
1/11 IBIT 26.63 BITO 22.33
7/12 +23.35% 32.85 -9.45% 20.22
BITOはこれに配当を加えなければならない 27.41 +22.75%
確かに現物にほぼ連動していると言えるな。。。サーセン(笑)
とは言え、先物が現物より高いのは間違いなく、先物を売って現物を買っていれば確実にサヤは抜ける。しかし、BITOを売り保有していてもサヤは抜けなかった、ということになる(空売りする場合は配当金を支払わなければならない)。
これは結局のところ現物と先物の価格差以上に価格が上がったから、と言えそうである、かな?(笑)いや、先物を売りの現物買いでは確実にサヤが抜けるのでやはり先物ETF特有の現象と言える。
先物ETFの場合日々ロールを繰り返すと仮定するとその日々の清算価格は現物価格ではなく上記で勘違いした決済ルールになるためここで価格のズレが起こる。つまり先物ETFの場合は清算価格が現物価格ではない、ということでよさそうだ。また、期近と期先の価格差が影響しそうにも思えるがそうではなく、やはり売却をする当該先物をいくらで買ったかに依拠するのだと思う。
現物より先物が高くても先物ETFが現物価格に連動するマジック
そこで7月の配当1.5がなぜこんなに高いか考えてみる
これはおそらく6月満期の先物の売却益だろう。この6月ものは5月に買われているはずだ。4月下旬から5月下旬にかけて期先にあたる6月ものを購入
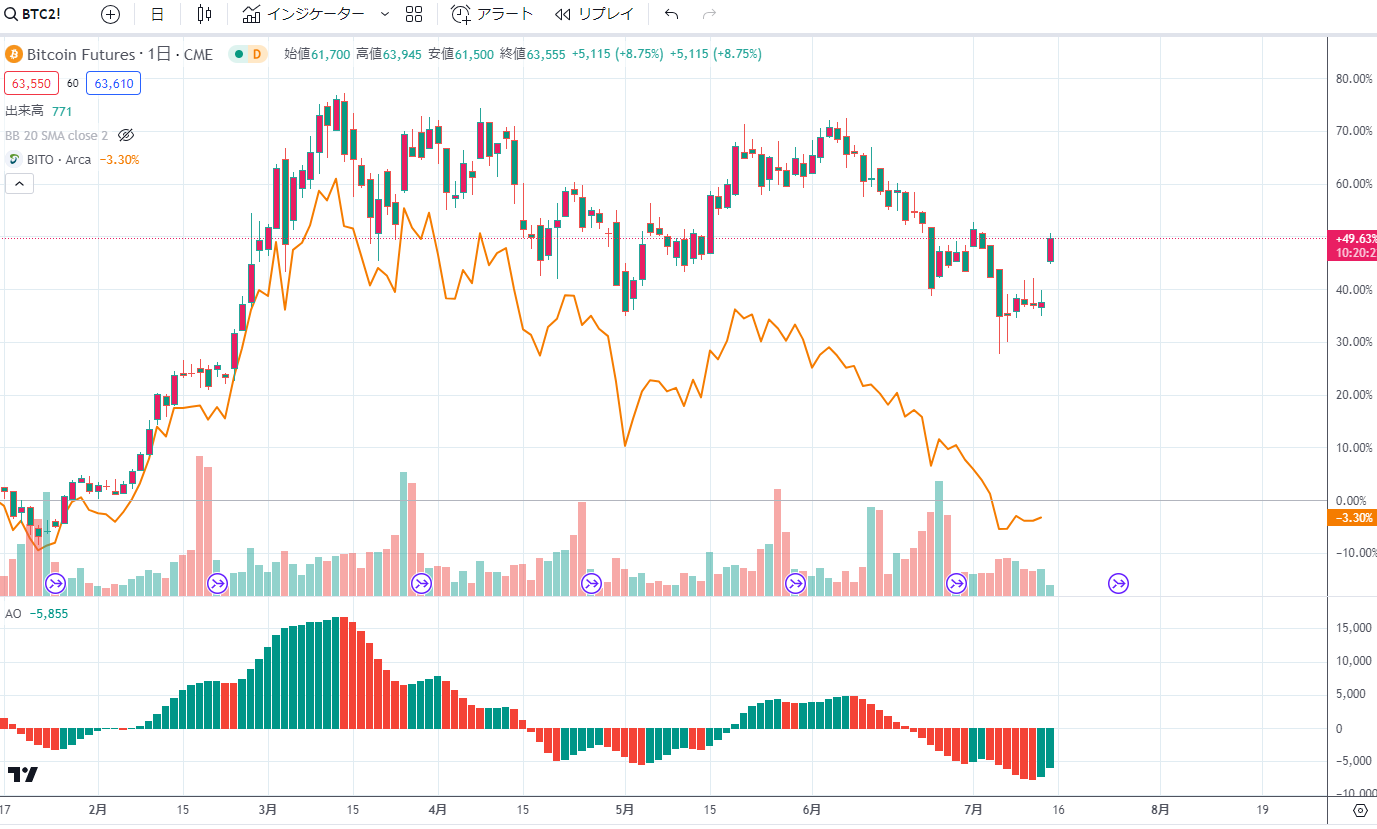
確かに4月下旬にかけて価格が下がってそこから5月下旬にかけてあがっている。この期間で取得価格の平均値がどれくらいで売却価格が平均どれくらいになるのか?ここで売却損益が決まってくるわけだがこんなに利益がでたのか?
先物ETFオプションの疑似合成先物売りと現物買いのサヤ取りは失敗
とは言え、肝心なのはオプションを使った合成疑似先物売りなので配当という観点では考慮しなくてよい。単純にETFの価格がどうなるかが焦点で先物売却益がETFに加算されないのでこれは売りにかなり優位性があることになるだろう。もちろんベースになる期近の先物価格が上がり続ければETF価格も上がり続けるが、現物の価格とどれくらい乖離するのか。この点BITOは先物ではないためまったく同様に考えることはできないが、少なくとも期先の価格が高ければ高いほど売りに優位性がでてきて現物と疑似先物売りでサヤは抜けることになる。
もっとも先物価格はVIX先物ほど高くない。せいぜい2%がいいところで年間2割かそれ以下のサヤを抜くよりもビットコインに投資したほうが利が大きそうだ、という元も子もないオチとなってしまう爆
CME CF ビットコイン参照レート
CME CF 暗号通貨ベンチマーク: よくある質問
https://www.bybit.com/ja-JP
https://crypto-media.jp/exchange-ranking-overseas/
海外の取引所でビットコインオプションをやるために
国内の取引所ではオプションはできないもよう。とりあえずbybitで取り急ぎ口座開設。
海外の取引所に入金する。これは結構やっかいな問題である。しかも暗号資産の取引においては規制が多い。
日本の取引所の場合は日本円で入金してビットコインを購入、売買するわけだが海外の取引所ではそもそも法定通貨を当該口座内で保有できない場合が多いらしい。つまり入り口の時点でなんらかの暗号資産、暗号通貨を入金する必要があるという。
しかし、常に暗号資産を持つというのは値動き激しすぎて不安な人も多いはずで、そういう意味でUSDTなどのステーブルコインに交換しておくという需要があるそうだ。
その点、日本人が日本の業者で取引する場合はその必要性はかなり乏しい。とは言え、日本で日本の業者を使ってUSDTは取引できない模様(笑)さすが金融後進国ジャパンである。
しかし、なぜ取引できないのかと言うと需要がないから、などというのは建前で要はアメリカ様の意向に沿っているようだ。米法案、中国製ブロックチェーンとテザーのUSDTの政府使用禁止を提案
もっとも、bybitはクレカでの入金(厳密にはクレカを使って暗号資産を買う)ができるのであまり問題ではないが、いかんせんその手数料がバカ高い。クレジットカードの手数料もさることながらレートそのものがめちゃくちゃ高めに設定されている(クレカ手数料も含んでいるのだろうか)。
クレカの手数料はパーセンテージなので購入金額が多くなればなるほど大変だ。仮に1000万円分入金しようとする4%で40万円である。さらにこれにぼったくりのレートが加算されてしまうからクレカは少額に限るべき。
取引手数料率(クレジットカード決済)

よって、オーソドックスに日本の取引所で暗号資産を買ってそれをbybitに送金するという方法がもっともコストがかからないことになる。
apple pay
アップルペイも使えるようになっているがこの場合の手数料は記載がない。とは言っても結局クレカで決済されるのだからクレカの手数料でいいということなのかもしれないが。
しかし、bybitの入金で使えないクレカはアップルペイをかますと使えたりするのかな?