- 投稿
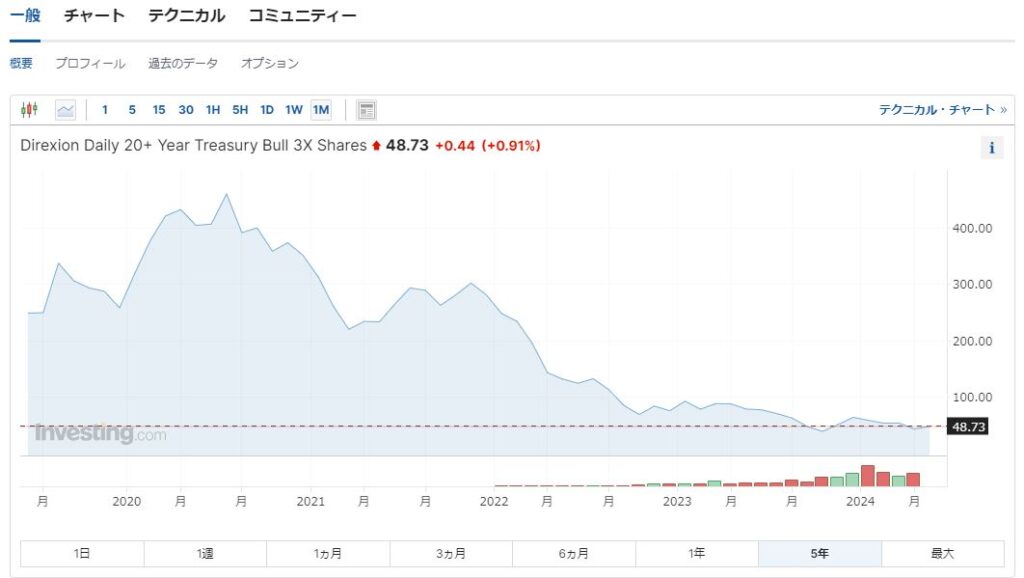
- 米国長期債に賭ける
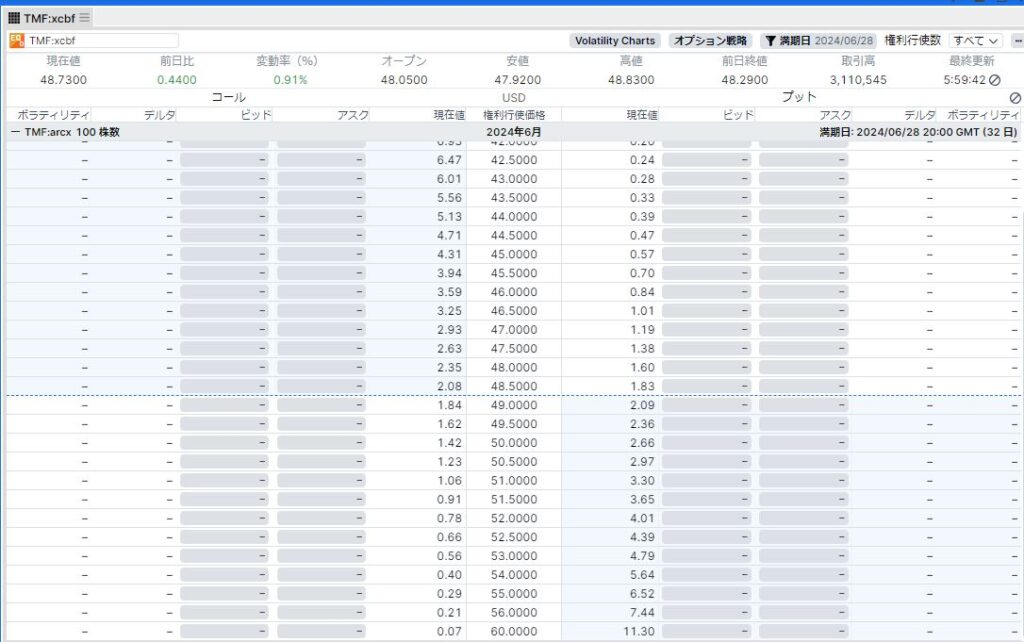
原資産直近終値 48.73
44@ 5.13 4.73-5.13 = 0.4 0.8%
45@ 4.31 3.73-4.31 = 0.6 1.23%
2020~2024/5/24日々騰落
平均 -0.093%
| 0.033546 | 413 | 428 | 36.39% | 37.71% |
| 0.067092 | 130 | 117 | 11.45% | 10.31% |
| 0.100638 | 17 | 20 | 1.50% | 1.76% |
| 5 | 5 | 0.44% | 0.44% | |
| 1135 | 565 | 570 | 49.78% | 50.22% |
年率(245)換算ボラ 51.65%
一か月(21)換算ボラ 15.37%
10% 54@ 0.4
下落相場にもかかわらず、日々の騰落率は半々になっている。高いところから下がった場合、もとに戻るにはそれ以上の上昇率が必要なため結果として原資産はマイナスになっているが。
今後長期金利が下落するとすれば長期債は上昇、そのETFも上昇することになるだろう。とは言え、ボラティリティがかなり高いため、下落する月の下落率も高いことが想定される。
原資産に投資できるだけの資金がないため、代替手段としてのオプションだが想定どおりのボラがでない場合なども考慮すると、単純なコール買い、プット売りは危険であることが分かる。
ディープインしたコールであれば上記のようにあまりコストをかけずに原資産を買ったのと同様のリターンを少ない資金で得られることとなるが、逆に言えば下落したときも同じような損失を被ることになり、その下落率がかなり大きいため一気に資金を失いかねない。
C45@ 4.31 P44@ 0.39
C46@ 3.59 P45@ 0.57
ATM C49@ 1.84 P48@ 1.6
C52@ 0.78
C53@ 0.56
C49@ 1.84 のみ
マイナス ×5 -9.2
プラス 2% -0.8×3 -2.4
10% 3.1×2 +6.2
30% 13×2 +26 or 20% 8×2 +16 計+20.6 or 10.6
P48@ 1.6 のみ
マイナス 5% 0.9×3 +2.7
15% 5.9×2 +11.8
プラス -1.6×7 -11.2 計 +3.3
C45@ 4.31のみ
マイナス 5% -3.31×3 -9.93
15% -4.31×2 -8.62
プラス 2% +0.4×3 +1.2
10% 4.4×2 +8.8
30% 14.4×2 +28.8 or 20% 9.4×2 +18.8 計+20.25 or 10.25
これからもボラが高いのであればATM付近をロングストラドルで利益は出そうであるが。。
レバレッジによる減価
2006年からの相対チャート
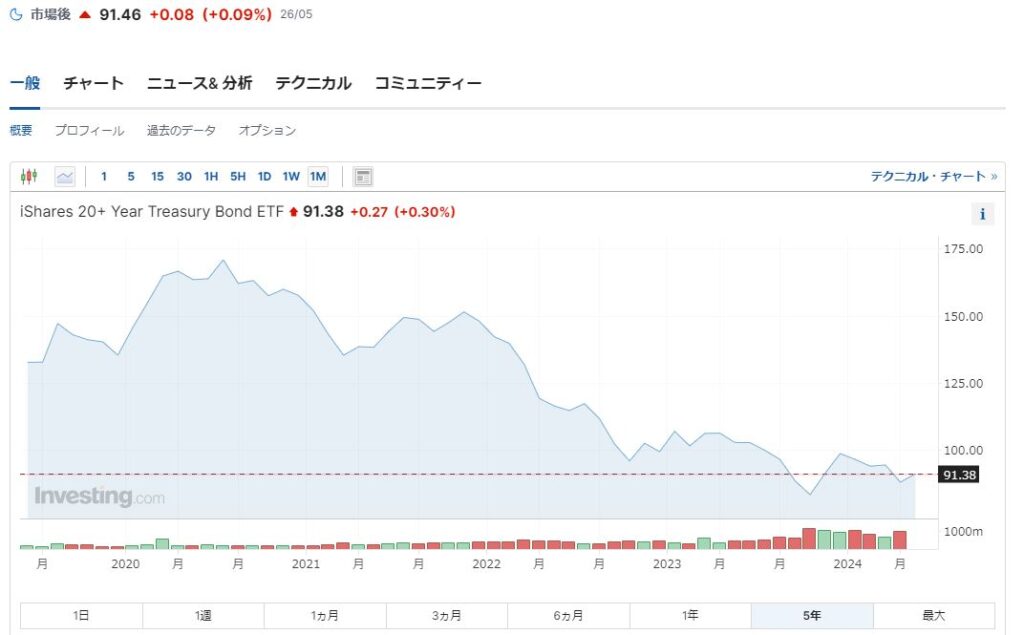
TLTはほとんど価格が変わっていないのにTMFはなんと-60%も減価している
オーマイガー
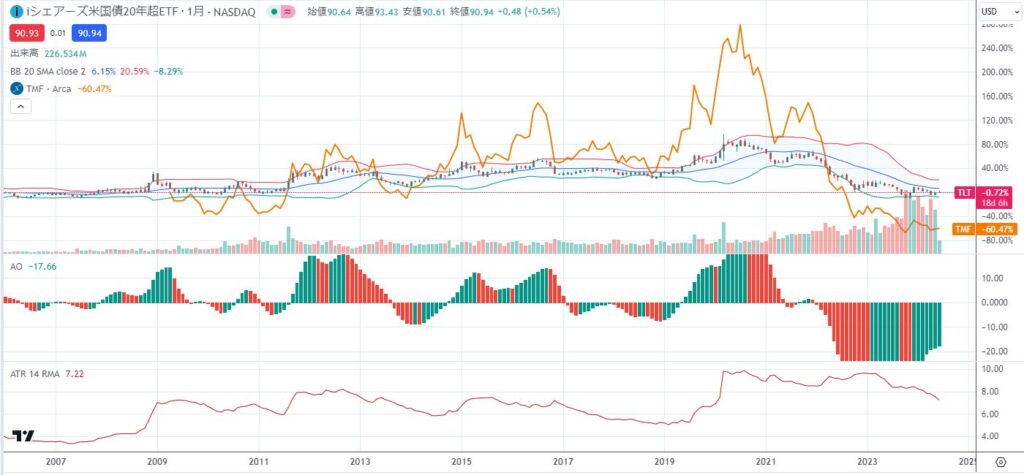
しかし、期間を変えてみると
2012年からは概ね理論値どおりのパフォーマンスに
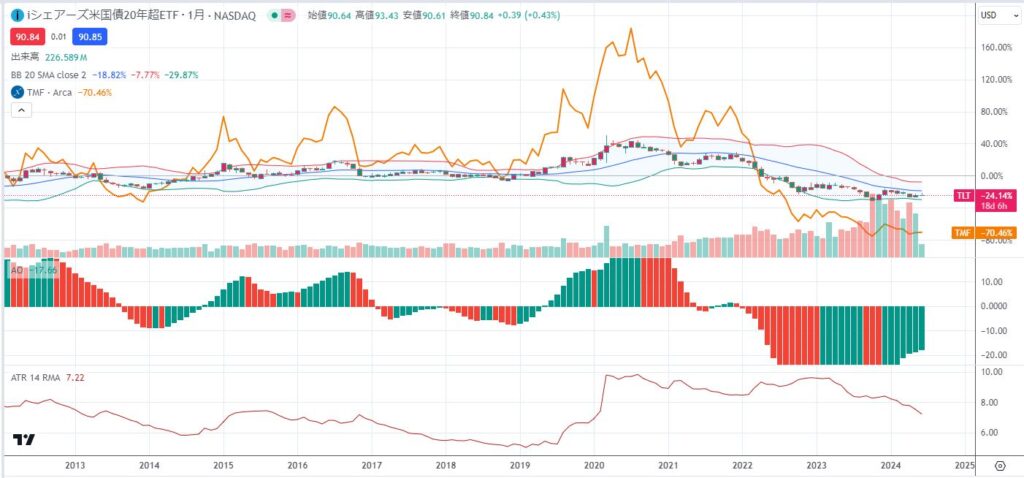
さらに2020年8月からをみると
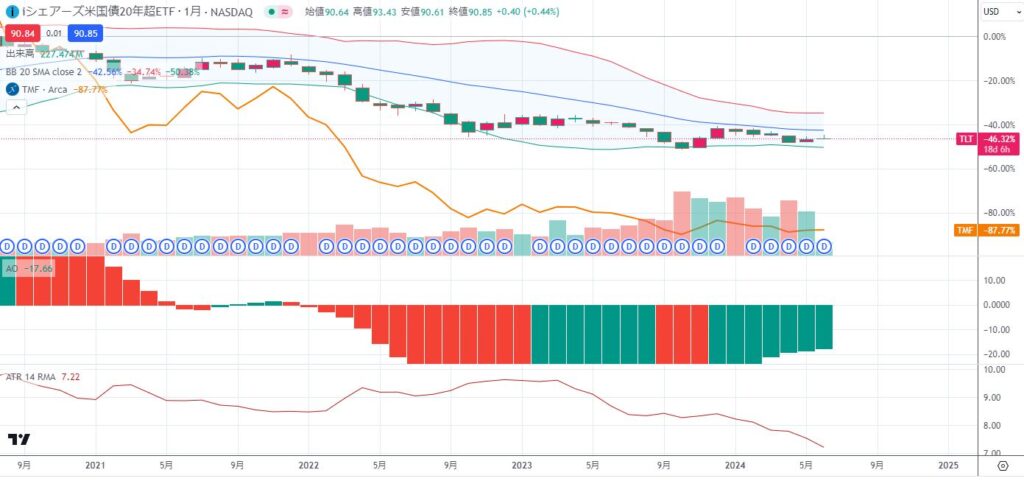
TLT-46%に対してTMFは-83%
TLTが-46%ならTMFは-138%となっていてもおかしくない、いやむしろそれ以上の下落率となっていそうだが
上下動を繰り返さない場合は減価しないどころかパフォーマンスはよくなるのは知られた話だが、このレバレッジによる増価効果とも言うべきものは原資産が下落する場合でも一方向に偏っている場合は発揮されるのか?
これは検証が必要だ
メンドクサイ(笑)
原資産の算出法
https://www.direxion.com/product/daily-20-year-treasury-bull-bear-3x-etfs
ICE 米国財務省 20 年超債券インデックス (IDCOT20) は、残存期間が 20 年を超える公募米国財務省証券を含む時価加重インデックスです。対象となる証券は、固定金利、米ドル建て、未償還額面 3 億ドル以上 (連邦準備銀行が保有する額を除く) である必要があります。インデックスから除外される証券は、インフレ連動証券、財務省短期証券、キャッシュ マネジメント短期証券、政府保証の有無にかかわらず発行された政府機関債務、およびクーポン支払い債券から剥奪されたゼロ クーポン発行です
TMFはTLTの3倍なわけで、端的にTLTというかICE 米国財務省 20 年超債券インデックスの算出方法を見ればいいことになるな
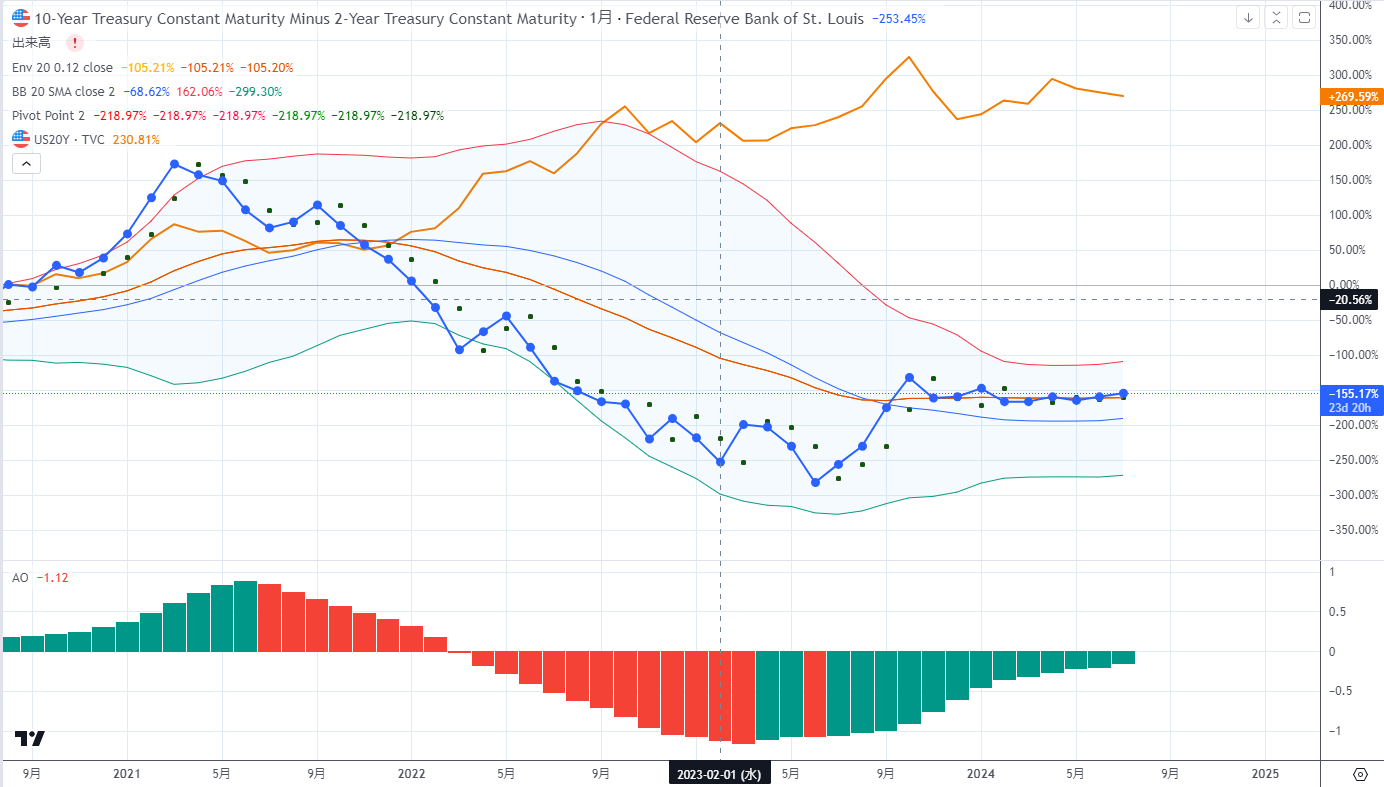
金利が下がれば債券は上がると単純に思っていたが果たしてそうか
例えば米国の政策金利が2%になったとしても長期金利が同様に下がるとは言えないだろう。もしかすると4%台で推移するかもしれない
そうなればTMFもとい、TLTというかICEの当該指数は上昇しない可能性もあるな
やはり同指数はどのような計算方法で算出されているのかを知っておかなければならない
TLTの価格 + 対m2の長期データ(こっちがメインになった)
買ったときから19年以下になるまでのリターンが積み重なったものがTLTの価格利回りは含まれないから無視
価格のリターンは、上の理論価格式だと、20 * (買ったときのyield - 売ったときのyield)
積み重ねると-20 * yieldをトラッキングする
リンク先が消えていたりしたので同指数が実際どのような算出方法をとっているか分からなかったが、恐らく考え方としては上記のようなものだろう
VIXの短期指数などもそうだが、指数として存続するには連続性がなければならないので現在の価格がいくらかというより騰落率を指数に加減算していくとみていいはずだ
債券の理論価格
その場合には「低金利近似」でおおよその債券の理論価格が算出できることになります。低金利近似の式を日本語で表すと(債券の現在価値変動率) = 満期までの年数 × 表面利回りと市場金利の金利差
となります。したがって、例えば満期が10年で市場金利が0.1%上昇すると債券価格はおおむね1%下落します。
満期が長いものや金利が高い局面ではこの近似は少々厳密な値とはズレますが、多くの場合にはこの「最終公式」さえ覚えていれば大体の債券の理論価格を計算できますので、ぜひ覚えておきましょう!
債券価格が安くなると当該債券の金利=利回りは上昇するが、ファンドとしては債券を保有して残存期間がある程度一定になるように(TLTだと20年超か)一定期間ごとに購入売却を繰り返してロールしているのだろう
そうすると買ったときよよりも債券価格が上がっていれば単純に指数にプラスされるということで、債券価格が上がっているということは金利=利回りが低下した(当該債券を買ったときより)ということになる